题目内容
已知函数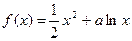 (a∈R).(1)若
(a∈R).(1)若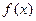 在[1,e]上是增函数,求a的取值范围(2)若a=1,a≤x≤e,证明:
在[1,e]上是增函数,求a的取值范围(2)若a=1,a≤x≤e,证明: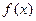 <
<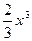
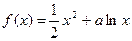 (a∈R).(1)若
(a∈R).(1)若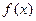 在[1,e]上是增函数,求a的取值范围(2)若a=1,a≤x≤e,证明:
在[1,e]上是增函数,求a的取值范围(2)若a=1,a≤x≤e,证明: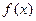 <
<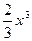
⑴a≥1,⑵略
(1)∵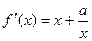 ,且在[1,e]上是增函数,∴
,且在[1,e]上是增函数,∴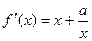 ≥0恒成立,
≥0恒成立,
即a≥-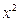 在[1,e]上恒成立, ∴a≥1……………… 6分
在[1,e]上恒成立, ∴a≥1……………… 6分
(2)证明:当a=1时,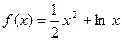 x∈[1,e].
x∈[1,e].

令F(x)=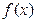 -
-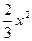 =
= -
-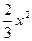 ,
,
∴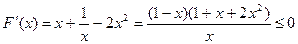 ,∴F(x) 在[1,e]上是减函数,
,∴F(x) 在[1,e]上是减函数,
∴F(x)≤F(1)=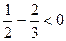 ∴x∈[1,e]时,
∴x∈[1,e]时,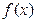 <
<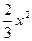 …………… 12分
…………… 12分
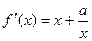 ,且在[1,e]上是增函数,∴
,且在[1,e]上是增函数,∴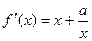 ≥0恒成立,
≥0恒成立,即a≥-
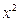 在[1,e]上恒成立, ∴a≥1……………… 6分
在[1,e]上恒成立, ∴a≥1……………… 6分(2)证明:当a=1时,
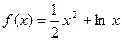 x∈[1,e].
x∈[1,e].

令F(x)=
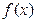 -
-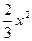 =
= -
-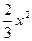 ,
, ∴
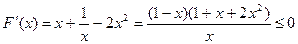 ,∴F(x) 在[1,e]上是减函数,
,∴F(x) 在[1,e]上是减函数,∴F(x)≤F(1)=
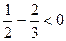 ∴x∈[1,e]时,
∴x∈[1,e]时,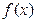 <
<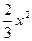 …………… 12分
…………… 12分
练习册系列答案
相关题目
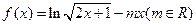 .
.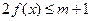 恒成立,求
恒成立,求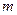 的取值范围.
的取值范围.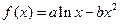 图象上一点
图象上一点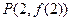 处的切线方程为
处的切线方程为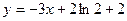 .
.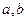 的值;(Ⅱ)若方程
的值;(Ⅱ)若方程 在
在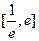 内有两个不等实根,求
内有两个不等实根,求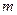 的取值范围(其中
的取值范围(其中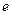 为自然对数的底数,
为自然对数的底数,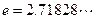 );
);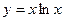 的单调递减区间是 ( )
的单调递减区间是 ( )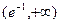

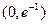
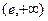
 R).(1)若
R).(1)若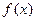 在
在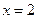 时取得极值,求
时取得极值,求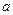 的值;
的值;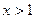 时,
时,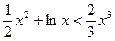 .
.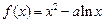 在
在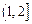 上是增函数,
上是增函数,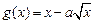 在
在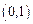 上是减函数.(1)求
上是减函数.(1)求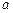 的值;(2)设函数
的值;(2)设函数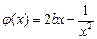 在
在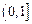 上是增函数,且对于
上是增函数,且对于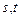 ,恒有
,恒有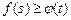 成立,求实数
成立,求实数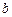 的取值范围;(3)设
的取值范围;(3)设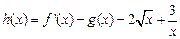 ,求证:
,求证: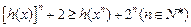 .
.
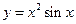 ,则
,则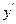 等于( )
等于( )



 定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.