题目内容
已知向量 =(cos
=(cos x,sin
x,sin x),
x), =(cosx,sinx)(0<x<π).设函数f(x)=
=(cosx,sinx)(0<x<π).设函数f(x)= •
• ,且f(x)+f'(x)为偶函数.
,且f(x)+f'(x)为偶函数.
(1)求x的值;
(2)求f(x)的单调增区间.
解:(1)f(x)= •
• =cos
=cos xcos?+sin
xcos?+sin xsin?=cos(
xsin?=cos( x-?),
x-?),
所以f(x)+f'(x)=cos( x-?)-
x-?)- sin(
sin( x-?)=2cos(
x-?)=2cos( x-?+
x-?+ ),
),
而f(x)+f'(x)为偶函数,则有-?+ =kπ,k∈Z,又0<?<π,则k=0,即?=
=kπ,k∈Z,又0<?<π,则k=0,即?= .
.
(2)由(1)得f(x)=cos( x-
x- ),由2kπ-π≤
),由2kπ-π≤ x-
x- ≤2kπ,
≤2kπ,
解得 (2kπ-
(2kπ- )≤x≤
)≤x≤ (2kπ+
(2kπ+ ),
),
即此函数的单调增区间为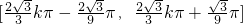 (k∈Z).
(k∈Z).
分析:(1)首先利用向量求得f(x),然后求出函数f(x)的导数,进而表示出f(x)+f'(x),再根据偶函数的定义求出结果;
(2)由(1)得出f(x)=cos( x-
x- ),再由余弦的单调性求出增区间即可.
),再由余弦的单调性求出增区间即可.
点评:本题考查了三角函数的化简、余弦的单调性以及偶函数的定义,平时要牢记三角函数的奇偶性和单调性,属于基础题.
 •
• =cos
=cos xcos?+sin
xcos?+sin xsin?=cos(
xsin?=cos( x-?),
x-?),所以f(x)+f'(x)=cos(
 x-?)-
x-?)- sin(
sin( x-?)=2cos(
x-?)=2cos( x-?+
x-?+ ),
),而f(x)+f'(x)为偶函数,则有-?+
 =kπ,k∈Z,又0<?<π,则k=0,即?=
=kπ,k∈Z,又0<?<π,则k=0,即?= .
.(2)由(1)得f(x)=cos(
 x-
x- ),由2kπ-π≤
),由2kπ-π≤ x-
x- ≤2kπ,
≤2kπ,解得
 (2kπ-
(2kπ- )≤x≤
)≤x≤ (2kπ+
(2kπ+ ),
),即此函数的单调增区间为
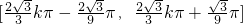 (k∈Z).
(k∈Z).分析:(1)首先利用向量求得f(x),然后求出函数f(x)的导数,进而表示出f(x)+f'(x),再根据偶函数的定义求出结果;
(2)由(1)得出f(x)=cos(
 x-
x- ),再由余弦的单调性求出增区间即可.
),再由余弦的单调性求出增区间即可.点评:本题考查了三角函数的化简、余弦的单调性以及偶函数的定义,平时要牢记三角函数的奇偶性和单调性,属于基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目