题目内容
函数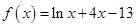 的零点一定位于区间( )
的零点一定位于区间( )
| A.(1, 2) | B.(2, 3) | C.(3, 4) | D.(4, 5) |
B
解析试题分析:因为 ,
, ,所以
,所以 ,根据根的存在性定理可知,函数
,根据根的存在性定理可知,函数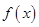 的零点在区间
的零点在区间 内.
内.
考点:零点存在性定理.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
设函数 ,则D(x) ( )
,则D(x) ( )
| A.是偶函数而不是奇函数 | B.是奇函数而不是偶函数 |
| C.既是偶函数又是奇函数 | D.既不是偶函数也不是奇函数 |
函数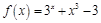 在区间
在区间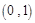 内的零点个数是( )
内的零点个数是( )
| A.0 | B.1 | C.2 | D.3 |
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
A.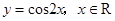 | B.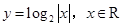 且 且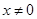 |
C.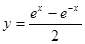 , ,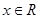 | D.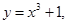 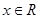 |
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为 ( )
A.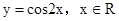 | B.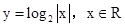 且x≠0 且x≠0 |
C.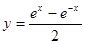 , x , x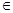 R R | D.y=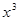 +1, x +1, x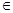 R R |
已知函数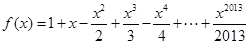 且函数
且函数 的零点均在区间
的零点均在区间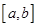
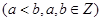 内,圆
内,圆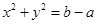 的面积的最小值是( )
的面积的最小值是( )
A.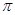 | B.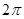 | C. | D.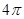 |
若 为奇函数且在
为奇函数且在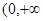 )上递增,又
)上递增,又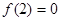 ,则
,则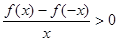 的解集是( )
的解集是( )
A. | B.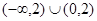 |
C.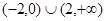 | D.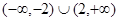 |
为了得到函数 的图象,可以把函数
的图象,可以把函数 的图象适当平移,这个平移是( )
的图象适当平移,这个平移是( )
A.沿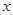 轴向右平移 轴向右平移 个单位 个单位 | B.沿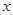 轴向右平移 轴向右平移 个单位 个单位 |
C.沿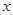 轴向左平移 轴向左平移 个单位 个单位 | D.沿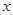 轴向左平移 轴向左平移 个单位 个单位 |
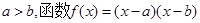 的图象如图,则函数
的图象如图,则函数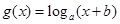 的图象可能为( )
的图象可能为( )