题目内容
抛物线C:x2=2y的焦点为F,过C上一点P(1,y0)的切线l与y轴交于点A,则|AF|=( )
分析:求出切线方程,确定A的坐标,求出焦点的坐标,即可得到结论.
解答:解:抛物线C:x2=2y可化为y=
求导数可得y′=x,当x=1时,y′=1,y=
,所以切线方程为y-
=x-1
令x=0,则y=-
,即A(0,-
)
∵抛物线C:x2=2y的焦点为F(0,
)
∴|AF|=1
故选C.
| x2 |
| 2 |
求导数可得y′=x,当x=1时,y′=1,y=
| 1 |
| 2 |
| 1 |
| 2 |
令x=0,则y=-
| 1 |
| 2 |
| 1 |
| 2 |
∵抛物线C:x2=2y的焦点为F(0,
| 1 |
| 2 |
∴|AF|=1
故选C.
点评:本题考查抛物线的几何性质,考查直线与抛物线的位置关系,属于基础题.

练习册系列答案
相关题目
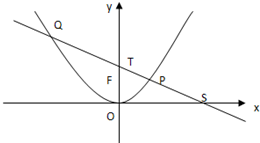 如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2).
如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2).