题目内容
如图,  是边长为
是边长为 的正方形,
的正方形, 平面
平面 ,
, ,
, ,
, 与平面
与平面 所成角为
所成角为 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)设点 是线段
是线段 上一个动点,试确定点
上一个动点,试确定点 的位置,使得
的位置,使得 平面
平面 ,并证明你的结论
,并证明你的结论

【答案】
(Ⅰ)证明:
因为 平面
平面 ,
,
所以 .
……………………2分
.
……………………2分
因为 是正方形,
是正方形,
所以 ,
,
从而 平面
平面 . ……………………4分
. ……………………4分
(Ⅱ)解:因为 两两垂直,
两两垂直,
所以建立空间直角坐标系 如图所示.
如图所示.
因为 与平面
与平面 所成角为
所成角为 ,即
,即 , ………………5分
, ………………5分
所以 .
.
由 可知
可知 ,
, .
………………6分
.
………………6分
则 ,
, ,
, ,
, ,
, ,
,
所以 ,
, ,
………………7分
,
………………7分
设平面 的法向量为
的法向量为
 ,则
,则 ,即
,即 ,
,
令 ,则
,则
 .
…………………8分
.
…………………8分
因为 平面
平面 ,所以
,所以 为平面
为平面 的法向量,
的法向量, ,
,
所以 .
…………………9分
.
…………………9分
因为二面角为锐角,所以二面角 的余弦值为
的余弦值为 . ………………10分
. ………………10分
(Ⅲ)解:点 是线段
是线段 上一个动点,设
上一个动点,设 .
.
则 ,
,
因为 平面
平面 ,
,
所以
 ,
…………………11分
,
…………………11分
即 ,解得
,解得 .
…………………12分
.
…………………12分
此时,点 坐标为
坐标为 ,
, ,符合题意. …………………13分
,符合题意. …………………13分
【解析】略

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
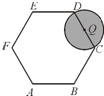 如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量
如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量| AP |
| AB |
| AF |
| A、(1,2] |
| B、[5,6] |
| C、[2,5] |
| D、[3,5] |
 如图,将边长为a的正方形剪去阴影部分后,围成一个正三棱锥,则正三棱锥的体积是
如图,将边长为a的正方形剪去阴影部分后,围成一个正三棱锥,则正三棱锥的体积是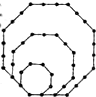 (2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是
(2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是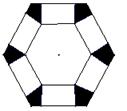
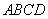 是边长为
是边长为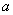 的正方形,以
的正方形,以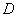 为圆心,
为圆心,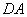 为半径的圆弧与以
为半径的圆弧与以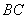 为直径的
为直径的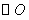 交于点
交于点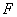 ,延长
,延长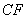 交
交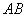 于
于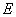 .(1)求证:
.(1)求证: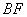 的长.
的长.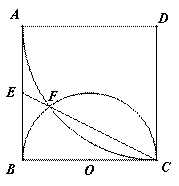
 ,若矩阵
,若矩阵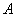 属于特征值3的一个特征向量为
属于特征值3的一个特征向量为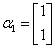 ,属于特征值-1的一个特征向量为
,属于特征值-1的一个特征向量为 ,求矩阵
,求矩阵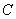 的极坐标方程为
的极坐标方程为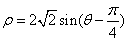 ,以极点为原点,极轴为
,以极点为原点,极轴为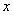 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线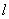 的参数方程为
的参数方程为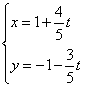 (
(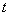 为参数),求直线
为参数),求直线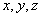 满足
满足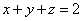 ,求
,求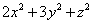 的最小值;
的最小值;