题目内容
5.从空间一点出发的三条射线PA,PB,PC均成60°角,则二面角B-PA-C的大小为( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $arcsin\frac{1}{3}$ | D. | $arccos\frac{1}{3}$ |
分析 取PA=PB=PC=2,PE=1,连接BE,CE,运用题目的条件得出∠BEC为二面角B-PA-C的平面角,△BEC中,BE=CE=$\sqrt{3}$,BC=2,运用余弦定理求解即可.
解答  解:取PA=PB=PC=2,PE=1,连接BE,CE
解:取PA=PB=PC=2,PE=1,连接BE,CE
∵∠BPE=∠CPE=60°,
∴△PBE≌△PCE,
∴BE=CE,
根据余弦定理得出:BE=CE=$\sqrt{3}$,
∴根据勾股定理判断出BE⊥PE,CE⊥PE,
∠BEC为二面角B-PA-C的平面角,
∵△BEC中,BE=CE=$\sqrt{3}$,BC=2,
∴cos∠BEC=$\frac{3+3-4}{2\sqrt{3}×\sqrt{3}}$=$\frac{1}{3}$,
∠BEC=$arccos\frac{1}{3}$.
故选:B.
点评 本题考查的知识点是二面角的平面角及求法,其中求出二面角的平面角转化为三角形中求解是解答本题的关键.

练习册系列答案
相关题目
15.曲线f(x)=exlnx+$\frac{{2{e^{x-1}}}}{x}$在点(1,f(1))处的切线方程为( )
| A. | ex-y+2-e=0 | B. | ex+y+2-e=0 | C. | ex-y+2+e=0 | D. | ex+y+2+e=0 |
20.下列各图中,可表示函数y=f(x)的图象的只可能是( )
| A. | 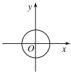 | B. | 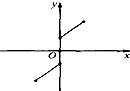 | C. |  | D. | 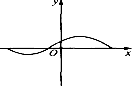 |
 已知函数f(x)=$\left\{\begin{array}{l}{x^2}+x,x<0\\{x^2}-x,x>0\end{array}$,
已知函数f(x)=$\left\{\begin{array}{l}{x^2}+x,x<0\\{x^2}-x,x>0\end{array}$,