题目内容
15.将函数y=sinx的图象向左平移$\frac{π}{4}$个单位,再将所得图象上各点的横坐标缩为原来的$\frac{1}{2}$,纵坐标不变,便得到函数f(x)的图象,则f(x)解析式为$f(x)=sin({2x+\frac{π}{4}})$.分析 利用y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:将函数y=sinx的图象向左平移$\frac{π}{4}$个单位,可得y=sin(x+$\frac{π}{4}$)的图象;
再将所得图象上各点的横坐标缩为原来的$\frac{1}{2}$,纵坐标不变,可得y=f(x)=sin(2x+$\frac{π}{4}$)的图象;
故f(x)解析式为f(x)=sin(2x+$\frac{π}{4}$),
故答案为:f(x)=sin(2x+$\frac{π}{4}$).
点评 本题主要考查诱导公式的应用,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
5.已知f(x)=$\left\{\begin{array}{l}{sin\frac{π}{2}x,x<0}\\{f(x-1)+2,x≥0}\end{array}\right.$,则f(2)=( )
| A. | 4 | B. | 7 | C. | 6 | D. | 5 |
6.若角α的终边与单位圆的交点为$P(\frac{12}{13},-\frac{5}{13})$,则tanα=( )
| A. | $\frac{5}{12}$ | B. | $-\frac{5}{12}$ | C. | $-\frac{12}{5}$ | D. | $\frac{12}{5}$ |
3.已知函数$f(x)=x+\frac{1}{x}({x≠0})$,命题p:?x>0,f(x)≥2,命题q:?x0<0,f(x0)≤-2,则下列判断正确的是( )
| A. | p是假命题 | B. | ¬q是真命题 | C. | p∨(¬q)是真命题 | D. | (¬p)∧q是真命题 |
10.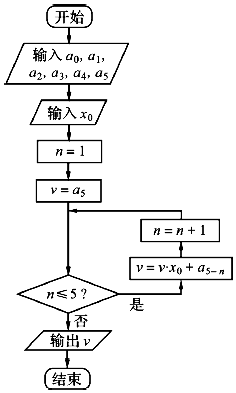 执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )
执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )
 执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )
执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )| A. | 15 | B. | 3 | C. | -3 | D. | -15 |
 如图,矩形ACEF和等边三角形ABC中,AC=2,CE=1,平面ABC⊥平面ACEF.M是线段EF上的一个动点.
如图,矩形ACEF和等边三角形ABC中,AC=2,CE=1,平面ABC⊥平面ACEF.M是线段EF上的一个动点. 如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈R,λ>0),
如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈R,λ>0),