Question

8．满足足约束条件$\left\{\begin{array}{l}{x≥0}\\{y≥3x}\\{4x+3y≤13}\end{array}\right.$，若不等式t²-$\frac{3}{2}$t≥4x-y恒成立，则实数t的取值范围（-∞，-$\frac{1}{2}$]∪[2，+∞）．

Answer 1

分析 问题转化为解不等式t²-$\frac{3}{2}$t≥（4x-y）_min即可，令z=4x-y，则y=4x-z，根据线性规划求出z的最大值，代入不等式求出即可．

解答 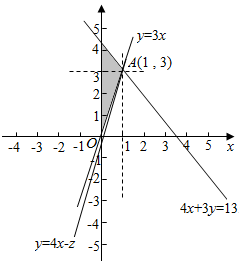解：若不等式t²-$\frac{3}{2}$t≥4x-y恒成立，
只需求出4x-y的最大值，解不等式t²-$\frac{3}{2}$t≥（4x-y）_min即可，
令z=4x-y，则y=4x-z，
画出满足条件的平面区域，如图示：
显然直线y=4x-z过A（1，3）时，
z最大，z的最大值是1，
故t²-$\frac{3}{2}$t≥1，解得：t≥2或t≤-$\frac{1}{2}$
故答案为：（-∞，-$\frac{1}{2}$]∪[2，+∞）．

点评 本题考查了简单的线性规划问题，考查解不等式问题，是一道中档题．