题目内容
矩形ABCD中,AD=2,AB≥AD,E为AD的中点,P是AB边上一动点.当∠DPE取得最大时,AP等于( )
分析:设AP=x,x>0,设∠DPE=θ,则易知0°<θ<60°,在△DPE中利用余弦定理可表示出cosθ,然后转化为求函数sinθ的最大值问题即可解决.
解答:解:设AP=x,则x>0,由题意知,DE=1,PE=
,PD=
,
可以看出三边中其中DE最短,所以其对应的∠DPE最小,设∠DPE=θ,则0°<θ<60°,
由余弦定理得:cosθ=
=
,
sin2θ=1-cos2θ=1-
=
,
因为sinθ在0°<θ<60°时为单调梯增函数,要使θ最大,即sinθ,最大就可,
sin2θ=
,而x2+
+5≥2
+5=9,
当且仅当x2=
即x=
时取等号.
则sin2θ≤
,所以sinθ≤
,当x=
时取等号,即θ取得最大值,
故选C.
| 1+x2 |
| 4+x2 |
可以看出三边中其中DE最短,所以其对应的∠DPE最小,设∠DPE=θ,则0°<θ<60°,
由余弦定理得:cosθ=
| (1+x2)+(4+x2)-1 | ||
2
|
| x2+2 | ||
|
sin2θ=1-cos2θ=1-
| (x2+2)2 |
| (1+x2)(4+x2) |
| x2 |
| (1+x2)(4+x2) |
因为sinθ在0°<θ<60°时为单调梯增函数,要使θ最大,即sinθ,最大就可,
sin2θ=
| 1 | ||
x2+
|
| 4 |
| x2 |
x2•
|
当且仅当x2=
| 4 |
| x2 |
| 2 |
则sin2θ≤
| 1 |
| 9 |
| 1 |
| 3 |
| 2 |
故选C.
点评:本题考查了余弦定理、函数最值的求解及函数思想,考查学生灵活运用所学知识解决问题的能力.

练习册系列答案
相关题目
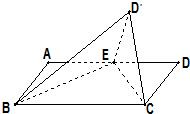 如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.
如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角. 如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE. 如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.设F为BD'的中点,证明:AF∥平面D'CE.
如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.设F为BD'的中点,证明:AF∥平面D'CE. 如图所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE
如图所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE