题目内容
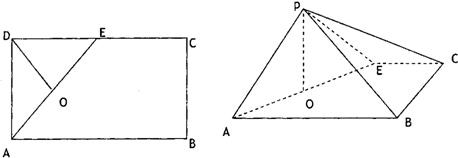
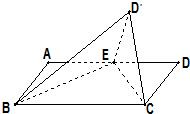 如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.
如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.(1)证明:BE⊥C D′;
(2)求二面角D′-BC-E的正切值.
分析:(1)欲证BE⊥CD′,先证BE⊥面D′EC,欲证线面垂直先证线线垂直,根据线面垂直的判定定理可证得;
(2)先以EB,EC为x、y轴,过E垂直平面BEC的射线为z轴,建立空间直角坐标系,设出平面D′BC的法向量,求出两平面的法向量的所成角的余弦值,再求出其正切值.
(2)先以EB,EC为x、y轴,过E垂直平面BEC的射线为z轴,建立空间直角坐标系,设出平面D′BC的法向量,求出两平面的法向量的所成角的余弦值,再求出其正切值.
解答: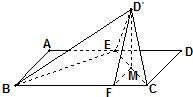 解:(1)∵AD=2AB=2,E是AD的中点,
解:(1)∵AD=2AB=2,E是AD的中点,
∴△BAE,△CDE是等腰直角三角形,
易知,∠BEC=90°,即BE⊥EC.
又∵平面D′EC⊥平面BEC,面D′EC∩面BEC=EC,
∴BE⊥面D′EC,又CD′?面D′EC,
∴BE⊥CD′.
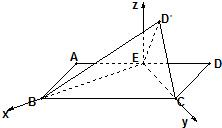 (2)如图以EB,EC为x、y轴,过E垂直平面BEC的射线为z轴,建立空间直角坐标系.
(2)如图以EB,EC为x、y轴,过E垂直平面BEC的射线为z轴,建立空间直角坐标系.
则B(
,0,0),C(0,
,0),D′(0,
,
),
=(-
,
,0),
=(0,
,-
),
设平面BEC的法向量为
=(0,0,1),平面D′BC的法向量为
=(x2,y2,z2),由
?
,
取x2=1,得
=(1,1,1),
∴cos<
,
>=
=
.
tan<
,
>=
,
∴二面角D′-BC-E的正切值为
.
 解:(1)∵AD=2AB=2,E是AD的中点,
解:(1)∵AD=2AB=2,E是AD的中点,∴△BAE,△CDE是等腰直角三角形,
易知,∠BEC=90°,即BE⊥EC.
又∵平面D′EC⊥平面BEC,面D′EC∩面BEC=EC,
∴BE⊥面D′EC,又CD′?面D′EC,
∴BE⊥CD′.
 (2)如图以EB,EC为x、y轴,过E垂直平面BEC的射线为z轴,建立空间直角坐标系.
(2)如图以EB,EC为x、y轴,过E垂直平面BEC的射线为z轴,建立空间直角坐标系.则B(
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| BC |
| 2 |
| 2 |
| D′C |
| ||
| 2 |
| ||
| 2 |
设平面BEC的法向量为
| n1 |
| n2 |
|
|
取x2=1,得
| n2 |
∴cos<
| n1 |
| n2 |
| ||||
|
|
| ||
| 3 |
tan<
| n1 |
| n2 |
| 2 |
∴二面角D′-BC-E的正切值为
| 2 |
点评:本题主要考查了平面与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
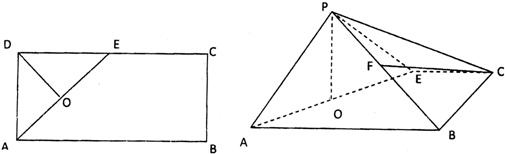 19、如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且PC=PB,F是BP的中点.
19、如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且PC=PB,F是BP的中点.
 如图所示,在矩形ABCD中,AB=4cm,BC=2cm,在图形上随机撒一粒黄豆,则黄豆落到圆上的概率是
如图所示,在矩形ABCD中,AB=4cm,BC=2cm,在图形上随机撒一粒黄豆,则黄豆落到圆上的概率是 如图所示,在矩形ABCD中,已知AB=a,BC=b.a≤3b,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且都等于x,则四边形EFGH面积的最大值为
如图所示,在矩形ABCD中,已知AB=a,BC=b.a≤3b,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且都等于x,则四边形EFGH面积的最大值为