题目内容
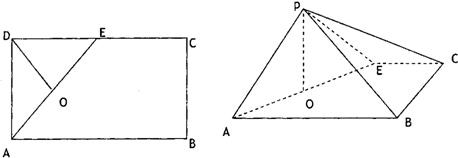
如图所示，在矩形ABCD中，AD=2AB=2，点E是AD的中点，将△DEC沿CE折起到△D′EC的位置，使二面角D′-EC-B是直二面角．设F为BD'的中点，证明：AF∥平面D'CE．
分析：欲证AF∥平面D'CE，根据直线与平面平行的判定定理可知只需证AF与平面D'CE内一直线平行即可，取CD'的中点P，连接FP，EP，利用平行四边形性质可知AF∥EP，而EP?面平面D'CE，AF?面平面D'CE，满足定理条件．
解答：
解：取CD'的中点P，连接FP，EP
∵F为BD'的中点，P为CD'的中点
∴FP
BC，
而点E是AD的中点，∴AE
BC，
∴FP
AE即四边形AFPE为平行四边形
∴AF∥EP，而EP?面平面D'CE，AF?面平面D'CE
∴AF∥平面D'CE．
解：取CD'的中点P，连接FP，EP∵F为BD'的中点，P为CD'的中点
∴FP
| ∥ |
. |
| 1 |
| 2 |
而点E是AD的中点，∴AE
| ∥ |
. |
| 1 |
| 2 |
∴FP
| ∥ |
. |
∴AF∥EP，而EP?面平面D'CE，AF?面平面D'CE
∴AF∥平面D'CE．
点评：本题主要考查了直线与平面平行的判定，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
相关题目
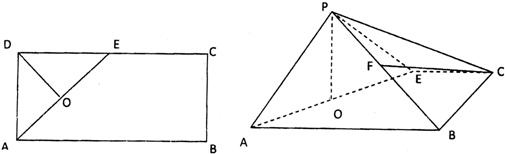19、如图所示，在矩形ABCD中，AB=4，AD=2，E是CD的中点，O为AE的中点，以AE为折痕将△ADE向上折起，使D到P点位置，且PC=PB，F是BP的中点．
如图所示，在矩形ABCD中，AB=4cm，BC=2cm，在图形上随机撒一粒黄豆，则黄豆落到圆上的概率是
如图所示，在矩形ABCD中，已知AB=a，BC=b．a≤3b，在AB，AD，CD，CB上分别截取AE，AH，CG，CF，且都等于x，则四边形EFGH面积的最大值为