题目内容
已知直线
，
．动圆（圆心为M）被
，
截得的弦长分别为8，16．
（Ⅰ）求圆心M的轨迹方程M；
（Ⅱ）设直线
与方程M的曲线相交于A，B两点．如果抛物线
上存在点N使得
成立，求k的取值范围．
同下
解析:
（Ⅰ）设
，M到
，
的距离分别为
，
，则
．2分
∴
，
∴
，即圆心M的轨迹方程M：． ……4分
（Ⅱ）设
，
，由
，
得
． ①
∴AB的中点为
， ………6分
∴AB的中垂线为
，即
， 7分
由
得
② …8分
∵存在N使得
成立的条件是：①有相异二解，并且②有解．…9分
∵①有相异二解的条件为
，
∴
且
． ③ …10分
②有解的条件是
，④ …11分
根据导数知识易得
时，
，
因此，由③④可得N点存在的条件是：
或
． ……12分
练习册系列答案
相关题目
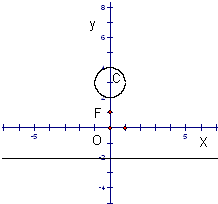如图，已知点F（0，1），直线L：y=-2，及圆C：x2+（y-3）2=1．
(a＞b＞0)经过点P(1，
)，且两焦点与短轴的一个端点构成等腰直角三角形．
n＝0(m，n∈R)．交椭圆C于A、B两点，求证：以AB为直径的动圆恒经过定点(0，1)．