题目内容
已知球的直径为10cm，求它的内接圆锥体积的最大值，并求出此时圆锥的底面半径和高．分析：设圆锥的底面半径为r，高为h，利用球心与截面圆心距，截面圆的半径球的半径满足的勾股定理，推出关系式，求出圆锥的体积表达式，利用导数求出函数的最大值．
解答：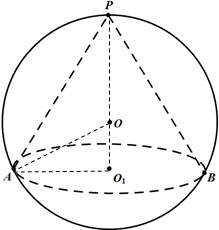
解：设圆锥的底面半径为r，高为h，则（h-5）2+r2=52
∴r2=10h-h2（2分）
V锥=
πr2h=
h(10h-h2)=
(10h2-h3) （5分）
V′=
(20h-3h2)，令V′=0，
h=
，（7分）
h∈(0，
)，V′(h)＞0；h∈(
，10)，V′(h)＜0
V（h）在（0，
）上是增函数，在（
，10）是奇函数，
当h=
时，V（h）最大（9分）
Vmax=
，（11分）
此时h=
，r=
（12分）
解：设圆锥的底面半径为r，高为h，则（h-5）2+r2=52∴r2=10h-h2（2分）
V锥=
| 1 |
| 3 |
| π |
| 3 |
| π |
| 3 |
V′=
| π |
| 3 |
h=
| 20 |
| 3 |
h∈(0，
| 20 |
| 3 |
| 20 |
| 3 |
V（h）在（0，
| 20 |
| 3 |
| 20 |
| 3 |
当h=
| 20 |
| 3 |
Vmax=
| 4000π |
| 81 |
此时h=
| 20 |
| 3 |
10
| ||
| 3 |
点评：本题考查空间想象能力，转化思想与计算能力，导数求解函数的最大值的方法．
练习册系列答案
相关题目
，求它的内接圆锥体积的最大值,并求出此时圆锥的底面半径和高. 
