题目内容
已知命题p:∀x1,x2∈R,(f(x2)-f(x1))(x2-x1)≥0,则綈p是( )
A.∃x1,x2∈R,(f(x2)-f(x1))(x2-x1)≤0
B .∀x1,x2∈R,(f(x2)-f(x1))
.∀x1,x2∈R,(f(x2)-f(x1)) (x2-x1)≤0
(x2-x1)≤0
C.∃x1,x2∈R,(f(x2)-f(x1))(x2-x1)<0
D.∀x1,x2∈R,(f(x2)-f(x1))(x2-x1)<0
C.利用“全称命题的否定是存在性命题”求解.命题p的否定为“∃x1,x2∈R,(f(x2)-f(x1))(x2-x1)<0 ”.
”.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 b,则角A等于
b,则角A等于 B.
B. C.
C.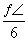 D.
D. ( )
( ) 人,从男生中选
人,从男生中选 人,从女生中选
人,从女生中选 人分别参加数学、物理、化学三科竞赛,共有
人分别参加数学、物理、化学三科竞赛,共有 种不同方案,那么男、女生人数分别是( )
种不同方案,那么男、女生人数分别是( ) ”是“sinx=
”是“sinx= ”的充分不必要条件;
”的充分不必要条件; =
= ,则sin(α+β)=___
,则sin(α+β)=___ _____.
_____.