题目内容
空间四边形ABCD中,AD=2,BC=1,AD、BC成60°角.M、N分别是AB、CD中点,求线段MN的长.
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:取BC中点P,连接PN,MP,可得NP=
,MP=1,∠MPN(或其补角)为AC与BD成的角,再利用余弦定理,可求MN.
| 1 |
| 2 |
解答:
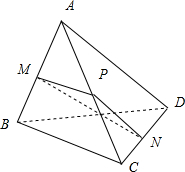 解:取AC中点P,连接PN,MP
解:取AC中点P,连接PN,MP
因为M,N分别为AB和CD的中点,所以PN和MP分别是△BCD和△ABC的中位线
所以NP
AD,MP
BC,
所以PN=1,MP=
,∴∠MPN(或其补角)为AC与BD成的角,
∵AD、BC成60°角,
∴∠MPN=60°或120°
根据余弦定理:MN2=MP2+NP2-2MP×NP×cos∠MPN
所以MN2=1+
-2×1×
×0.5=
或MN2=1+
+2×1×
×0.5=
,
所以MN=
或
.
 解:取AC中点P,连接PN,MP
解:取AC中点P,连接PN,MP因为M,N分别为AB和CD的中点,所以PN和MP分别是△BCD和△ABC的中位线
所以NP
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
所以PN=1,MP=
| 1 |
| 2 |
∵AD、BC成60°角,
∴∠MPN=60°或120°
根据余弦定理:MN2=MP2+NP2-2MP×NP×cos∠MPN
所以MN2=1+
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |
所以MN=
| ||
| 2 |
| ||
| 2 |
点评:本题考查异面直线所成的角,考查余弦定理的运用,考查学生的计算能力,正确作出异面直线所成的角是关键.

练习册系列答案
相关题目
函数f(x)=
+ln
的零点所在的大致区间是( )
| 2 |
| x |
| 1 |
| x-1 |
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(1,2)与(2,3) |
将6名教师4名学生平均分成2个小组(每个小组的学生数相同),分别安排到甲、乙两地参加社会实践活动,则不同的安排方案的种数为( )
| A、40 | B、60 |
| C、120 | D、240 |
 一个几何体的三视图如图所示,则该几何体的体积可能是
一个几何体的三视图如图所示,则该几何体的体积可能是