题目内容
在△ABC中,有命题
①
-
=
;
②
+
+
=
;
③若(
+
)•(
-
)=0,则△ABC为等腰三角形;
④若
•
>0,则△ABC为锐角三角形.
上述命题正确的是( )
①
| AB |
| AC |
| BC |
②
| AB |
| BC |
| CA |
| 0 |
③若(
| AB |
| AC |
| AB |
| AC |
④若
| AC |
| AB |
上述命题正确的是( )
| A、①② | B、①④ | C、②③ | D、②③④ |
分析:利用向量的运算法则;锐角三角形需要三个角全为锐角.
解答:解:由向量的运算法则知
-
=
;
+
+
=
故①错②对
又(
+
)•(
-
)=
2-
2
∵(
+
)•(
-
)=0
∴
2=
2即AB=AC
∴△ABC为等腰三角形故③对
∵
•
>0
∴∠A为锐角但三角形不是锐角三角形
故选项为C
| AB |
| AC |
| CB |
| AB |
| BC |
| CA |
| 0 |
又(
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
∵(
| AB |
| AC |
| AB |
| AC |
∴
| AB |
| AC |
∴△ABC为等腰三角形故③对
∵
| AC |
| AB |
∴∠A为锐角但三角形不是锐角三角形
故选项为C
点评:考查向量的运算法则.

练习册系列答案
相关题目
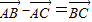 ;
;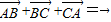 ;
;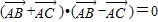 ,则△ABC为等腰三角形;
,则△ABC为等腰三角形;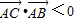 ,则△ABC为钝角三角形.
,则△ABC为钝角三角形.