题目内容
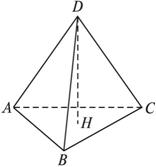
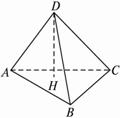
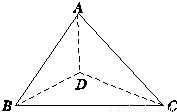
已知△ADB和△ADC都是以D为直角顶点的直角三角形,且AD=BD=CD,∠BAC=60°.(1)求证:BD⊥平面ADC;
(2)若H是△ABC的垂心,求证:H是D在平面ABC内的射影.
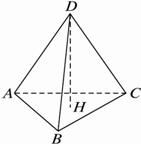
证明:(1)不妨设AD=BD=CD=1,则AB=AC=![]() ,
,
![]() ·
·![]() =(
=(![]() -
-![]() )·
)·![]() =
=![]() ·
·![]() -
-![]() ·
·![]() .?
.?
由于![]() ·
·![]() =
=![]() ·(
·(![]() +
+![]() )=
)=![]() ·
·![]() =1,
=1,
及![]() ·
·![]() =|
=|![]() ||
||![]() |cos60°=
|cos60°=![]() ·
·![]() ·
·![]() =1,
=1,
∴![]() ·
·![]() =0,即BD⊥AC,而已知BD⊥AD.
=0,即BD⊥AC,而已知BD⊥AD.
∴BD⊥平面ADC.
(2)![]() ·
·![]() =(
=(![]() +
+![]() )·
)·![]() =
=![]() ·
·![]() =
=![]() ·
·![]() =
=![]() ·(
·(![]() -
-![]() )=
)= ![]() ·
·![]() -
-![]() ·
·![]() =1·
=1·![]() ·cos45°-1·
·cos45°-1·![]() ·cos45°=0.∴DH⊥BC.
·cos45°=0.∴DH⊥BC.
又![]() ·
·![]() =(
=(![]() -
-![]() )·
)·![]() =BH·
=BH·![]() -
-![]() ·
·![]() =0,∴DH⊥AC,从而DH⊥平面ABC,即H是D在平面ABC上的射影.
=0,∴DH⊥AC,从而DH⊥平面ABC,即H是D在平面ABC上的射影.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
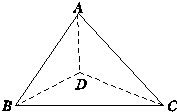 如图所示,已知△ADB和△ADC都是以D为直角顶点的直角三角形,且AD=BD=CD,∠BAC=60°.求证:BD⊥平面ADC.
如图所示,已知△ADB和△ADC都是以D为直角顶点的直角三角形,且AD=BD=CD,∠BAC=60°.求证:BD⊥平面ADC.