题目内容
已知数列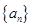 的前
的前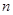 项和
项和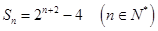 ,函数
,函数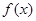 对
对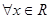 有
有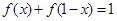 ,数列
,数列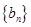 满足
满足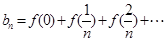
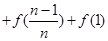 .
.
(1)分别求数列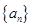 、
、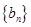 的通项公式;
的通项公式;
(2)若数列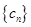 满足
满足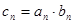 ,
,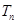 是数列
是数列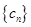 的前
的前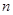 项和,若存在正实数
项和,若存在正实数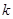 ,使不等式
,使不等式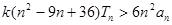 对于一切的
对于一切的 恒成立,求
恒成立,求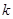 的取值范围.
的取值范围.
(1) (2)
(2)
解析试题分析:(1)由数列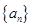 的前
的前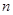 项和
项和 求
求 ,分两种情况进行,
,分两种情况进行,  时
时 和
和 时,
时,  .数列
.数列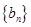 利用
利用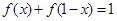 可求得.
可求得.
(2)由(1)得 ,
, 利用
利用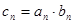 得出
得出 关系式,利用错位相减法得出
关系式,利用错位相减法得出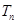 ,再利用参数分离法得出k的范围.
,再利用参数分离法得出k的范围.
试题解析:(1)  1分
1分
 时满足上式,故
时满足上式,故 3分
3分
∵ =1∴
=1∴ 4分
4分
∵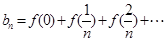
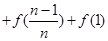 ①
①
∴
 ②
②
∴①+②,得 6分
6分
(2) 
 7分
7分 ①
①
 ②
②
①-②得 8分
8分
即  10分
10分
要使得不等式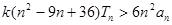 恒成立,
恒成立, 对于一切的
对于一切的 恒成立,
恒成立,
即 11分
11分
令 ,则
,则
当且仅当 时等号成立,故
时等号成立,故 13分
13分
所以 为所求. 14分
为所求. 14分
考点:已知 求
求 ,错位相减法,参数分离.
,错位相减法,参数分离.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
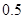 万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变. ,每年发放的电动型汽车牌照数为构成数列
,每年发放的电动型汽车牌照数为构成数列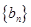 ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;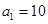
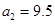
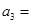
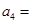
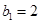

 3
3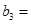
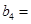
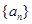 中,
中,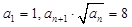 .
.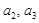 ;
;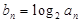 ,求证:
,求证: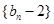 为等比数列;
为等比数列;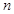 项积
项积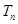 .
.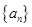 、
、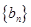 中,
中, ,且当
,且当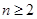 时,
时,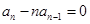 ,
,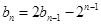 .记
.记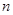 的阶乘
的阶乘 .
.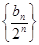 为等差数列;
为等差数列;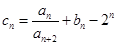 ,求
,求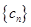 的前
的前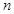 项和.
项和.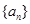 的前
的前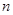 项和为
项和为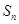 ,
,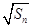 是
是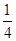 与
与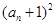 的等比中项.
的等比中项.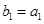 ,且
,且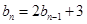 ,求数列
,求数列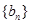 的通项公式;
的通项公式;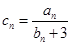 ,求数列
,求数列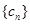 的前
的前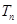 .
. 满足
满足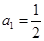 ,
,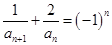
 .
.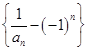
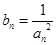
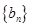 的前
的前 项和
项和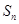 ;
;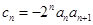 ,数列
,数列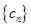 的前
的前 ,求证:
,求证: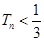 (其中
(其中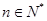 ).
).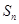 表示等差数列
表示等差数列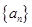 的前
的前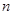 项的和,且
项的和,且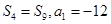
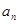 及
及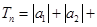 ……
……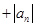
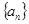 满足:
满足: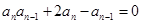 ,
, 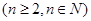 ,
, ,前
,前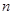 项和为
项和为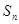 的数列
的数列 满足:
满足: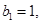
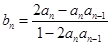
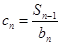
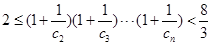
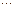 +
+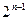 所有项的和为
所有项的和为