题目内容
3.已知m=|a+b|+|a-b|,则以下不等式恒成立的是( )| A. | m≤2|a| | B. | m≤2|b| | C. | m≥2|a| | D. | m≥2(|a|+|b|) |
分析 由条件利用绝对值三角不等式,可得结论.
解答 解:∵m=|a+b|+|a-b|,利用绝对值三角不等式可得m≥|(a+b)+(a-b)|=2|a|,
故选:C.
点评 本题主要考查绝对值三角不等式的应用,函数的恒成立问题,属于基础题.

练习册系列答案
相关题目
11.已知函数f(x)=$\left\{\begin{array}{l}{-1,x为有理数}\\{1,x为无理数}\end{array}\right.$,若直线x=a是函数f(x)图象的对称轴,则( )
| A. | a是整数 | B. | a是无理数 | C. | a是有理数 | D. | a不存在 |
15.二次函数f(x)满足f(x-2)=f(-x-2),且其图象在y轴上的截距为1,在x轴上截得的线段长为$\sqrt{2}$,则f(x)的解析式为( )
| A. | x2+$\frac{8}{7}$x+1 | B. | $\frac{2}{7}$x2+x+1 | C. | $\frac{2}{7}$x2+$\frac{8}{7}$x | D. | $\frac{2}{7}$x2+$\frac{8}{7}$x+1 |
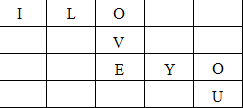 将“I LOVE YOU”8个英文字母填入5×4的方格中,其中“I“字母填入左上角,“U”字母填入右下角,将其余6个英文字母依次填入方格,要求只能横读或竖读成一句原话,如图所示为一种填法,则共有35种不同的填法.(用数字作答)
将“I LOVE YOU”8个英文字母填入5×4的方格中,其中“I“字母填入左上角,“U”字母填入右下角,将其余6个英文字母依次填入方格,要求只能横读或竖读成一句原话,如图所示为一种填法,则共有35种不同的填法.(用数字作答)