题目内容
 如图,
如图,| AB |
| BC |
| CD |
(1)若
| BC |
| AD |
(2)在(1)的条件下,若又有
| AC |
| BD |
分析:(1)首先用向量AB,BC,CD表示出向量AD,然后根据
∥
的条件,得出结果.
(2)先表示出向量AC,BD,再由
⊥
,求出向量AC,BD的坐标,进而求出面积.
| BC |
| AD |
(2)先表示出向量AC,BD,再由
| AC |
| BD |
解答:解:(1)由
=
+
+
=(4+x,y-2),(2分)
∥
?x(y-2)-y(4+x)=0?x+2y=0①(5分)
(2)
=(x+6,y+1),
=(x-2,y-3)(6分)
⊥
?(x+6)(x-2)+(y+1)(y-3)=0?x2+y2+4x-2y-15=0②(8分)
解①②得
或
(舍),∴
=(8,0),
=(0,-4),(10分)
由
⊥
知:SABCD=
|
|•|
|=16.(12分)
| AD |
| AB |
| BC |
| CD |
| BC |
| AD |
(2)
| AC |
| BD |
| AC |
| BD |
解①②得
|
|
| AC |
| BD |
由
| AC |
| BD |
| 1 |
| 2 |
| AC |
| BD |
点评:本题考查了向量平行和垂直的条件,只要牢记条件问题就会迎刃而解,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
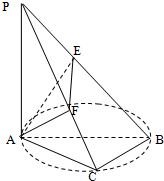 如图,AB是圆O的直径,C是圆O上的点,PA垂直于圆O所在平面,AE⊥PB于E,AF⊥PC于F
如图,AB是圆O的直径,C是圆O上的点,PA垂直于圆O所在平面,AE⊥PB于E,AF⊥PC于F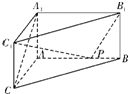 (2012•蓝山县模拟)如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥AC,AC=AA1=1,P为线段AB上的动点.
(2012•蓝山县模拟)如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥AC,AC=AA1=1,P为线段AB上的动点. 已知如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°.
已知如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°.