题目内容
12.为了检测某种产品的质量,抽取了一个容量为100的样本,数据的分组数如下:[10.75,10.85)3;[10.85,10.95)9;[10.95,11.05)13;[11.05,11.15)16;[11.15,11.25)26;[11.25,11.35)20;[11.35,11.45)7;[11.45,11.55)4;[11.55,11.65)2;
(1)列出频率分布表含累积频率;
(2)画出频率分布直方图以及频率分布折线图;
(3)据上述图表,估计数据落在[10.95,11.35)范围内的可能性是百分之几?
分析 (1)根据题目中数据进行列表,根据频率=$\frac{频数}{样本容量}$求出每组的频率,画出频率分布表即可;
(2)根据用频率除以组距,得到频率分布直方图的纵坐标,然后画出频率分布直方图,最后将矩形的中点连起来得到频率分布折线图;
(3)根据频率分布表中的数据求出落在[10.95,11.35)范围内的频率,从而得到数据落在[10.95,11.35)范围内的可能性;
解答 解:(1)频率分布表如图所示:
| 分组 | 频数 | 频率 | 累积频率 |
| [10.75,10.85) | 3 | 0.03 | 0.03 |
| [10.85,10.95) | 9 | 0.09 | 0.12 |
| [10.95,11.05) | 13 | 0.13 | 0.25 |
| [11.05,11.15) | 16 | 0.16 | 0.41 |
| [11.15,11.25) | 26 | 0.26 | 0.67 |
| [11.25,11.35) | 20 | 0.20 | 0.87 |
| [11.35,11.45) | 7 | 0.07 | 0.94 |
| [11.45,11.55) | 4 | 0.04 | 0.98 |
| [11.55,11.65) | 2 | 0.02 | 1.00 |
| 合计 | 100 | 1.00 |
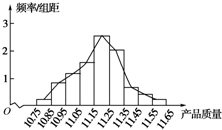
(3)由上述图表可知数据落在[10.95,11.35)范围内的频率为1-(0.03+0.09)-(0.07+0.04+0.02)=0.75=75%,
即数据落在[10.95,11.35)范围内的可能性是75%;
点评 本题主要考查了频率分布表,以及概率问题,统计初步在近两年高考中每年都以小题的形式出现,基本上是低起点题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
17.设锐角△ABC的三个内角A,B,C所对的边分别为a,b,c,且b=3,c=1,△ABC的面积为$\sqrt{2}$,则a的值为( )
| A. | 2$\sqrt{2}$或2$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{6}$ |
1.设命题p:函数y=sin2x的最小正周期为$\frac{π}{2}$,命题q:函数y=cosx的图象关于直线x=$\frac{π}{2}$对称,则下列判断正确的是( )
| A. | p为真 | B. | q为真 | C. | p∧q为假 | D. | p∨q为真 |
2.已知函数f(x)=2x-x-2的一个零点所在的区间是( )
| A. | (-1,0) | B. | (0,1) | C. | (1,3) | D. | (3,4) |