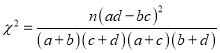题目内容
【题目】已知![]() .
.
(I)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程.
处的切线方程.
(II)若![]() ,求函数
,求函数![]() 的单调区间.
的单调区间.
(III)若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ) ![]() ;(Ⅱ)答案见解析;(Ⅲ)
;(Ⅱ)答案见解析;(Ⅲ) ![]() .
.
【解析】试题分析:(1)由题意易得![]() ,
, ![]() ,根据点斜式得到曲线
,根据点斜式得到曲线![]() 在点
在点![]() 处的切线方程;(2)
处的切线方程;(2)![]() ,对
,对![]() 分类讨论明确相应不等式的解集,即可得到函数
分类讨论明确相应不等式的解集,即可得到函数![]() 的单调区间;(3)不等式
的单调区间;(3)不等式![]() 恒成立等价于
恒成立等价于![]() 在
在![]() 上恒成立,变量分离即
上恒成立,变量分离即![]() 在
在![]() 上恒成立。转求
上恒成立。转求![]() 的最大值即可.
的最大值即可.
试题解析:
(I)∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,所有切点坐标为
,所有切点坐标为![]() .
.
∴所求切线方程为![]() ,
,
即![]() .
.
(II)![]() ,
,
由![]() ,得
,得![]() 或
或![]() .
.
(![]() )当
)当![]() 时,由
时,由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]() 或
或![]() ,
,
此时![]() 的单调递减区间为
的单调递减区间为![]() ,
,
单调递增区间为![]() 和
和![]() .
.
(![]() )当
)当![]() 时,由
时,由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]() 或
或![]() .
.
此时![]() 的单调递减区间为
的单调递减区间为![]() ,
,
单调递增区间为![]() 和
和![]() .
.
综上:当![]() 时,
时, ![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() 和
和![]() ;
;
当![]() 时,
时, ![]() 的单调递减区间为
的单调递减区间为![]() ,
,
单调递增区间为![]() 和
和![]() .
.
(III)依题意![]() ,不等式
,不等式![]() 恒成立,
恒成立,
等价于![]() 在
在![]() 上恒成立,
上恒成立,
可得![]() 在
在![]() 上恒成立,
上恒成立,
设![]() ,
,
则![]() .
.
令![]() ,得
,得![]() ,
, ![]() (舍),
(舍),
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ,
,
当![]() 变化时,
变化时, ![]() ,
, ![]() 变化情况如下表:
变化情况如下表:
|
|
|
|
|
|
|
|
| 单调递增 |
| 单调递减 |
∴当![]() 时,
时, ![]() 取得最大值,
取得最大值,
![]() ,∴
,∴![]() .
.
∴![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某校随机调查了80位学生,以研究学生中爱好羽毛球运动与性别的关系,得到下面的数据表:
爱好 | 不爱好 | 合计 | |
男 | 20 | 30 | 50 |
女 | 10 | 20 | 30 |
合计 | 30 | 50 | 80 |
(1)将此样本的频率估计为总体的概率,随机调查了本校的3名学生.设这3人中爱好羽毛球运动的人数为![]() ,求
,求![]() 的分布列和期望值;
的分布列和期望值;
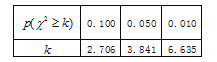
(2)根据表中数据,能否有充分证据判定爱好羽毛球运动与性别有关联?若有,有多大把握?
附: