题目内容
已知函数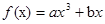 ,(
,(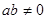 ),对任意
),对任意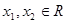 且
且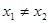 都有
都有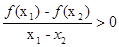 ,若
,若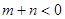 ,则
,则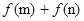 的值( )
的值( )
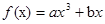 ,(
,(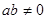 ),对任意
),对任意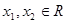 且
且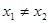 都有
都有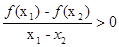 ,若
,若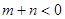 ,则
,则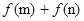 的值( )
的值( )| A.恒大于0 | B.恒小于0 | C.可能为0 | D.可正可负 |
B
试题分析:由
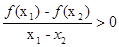 可知
可知 单调递增,所以若
单调递增,所以若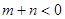 ,则
,则 ,所以
,所以 ,又很容易可以判断出函数
,又很容易可以判断出函数 是奇函数,所以
是奇函数,所以 ,所以
,所以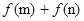 的值横小于0.
的值横小于0.点评:函数的单调性和奇偶性是函数的比较重要的两条性质,经常结合在一起考查,要注意对这两条性质准确掌握并灵活运用.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
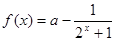 .
.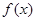 的单调性;
的单调性;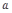 的值;
的值;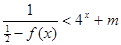 对
对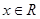 恒成立,求实数
恒成立,求实数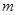 的取值范围.
的取值范围.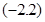 上的奇函数
上的奇函数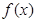 ,满足
,满足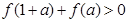 ,又当
,又当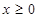 时,
时,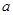 的取值范围。
的取值范围。 的值域是 .
的值域是 .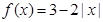 ,
,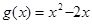 ,
,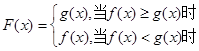 ,则
,则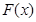 的最值是( )
的最值是( )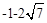
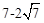 ,无最小值
,无最小值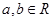 ,且
,且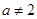 ,定义在区间
,定义在区间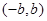 内的函数
内的函数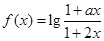 是奇函数.
是奇函数.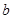 的取值范围;
的取值范围;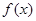 的单调性并证明.
的单调性并证明.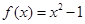 ,对任意
,对任意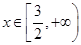 ,
,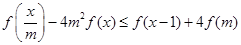 恒成立,则实数
恒成立,则实数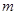 的取值范围是
的取值范围是 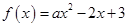 在
在 上是减函数,则
上是减函数,则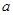 的取值范围是( )
的取值范围是( )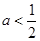
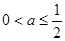
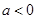 或
或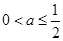
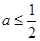
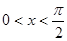 时,函数
时,函数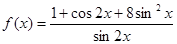 的最小值为
的最小值为