题目内容
11.已知M={-$\frac{1}{2}$,3},N=(x|mx=1},若N⊆M,则适合条件的实数m构成的集合P为( )| A. | {-2,$\frac{1}{3}$} | B. | {-$\frac{1}{2}$,$\frac{1}{3}$} | C. | {0,-2,$\frac{1}{3}$} | D. | {0} |
分析 由N⊆M,可分N=∅和N≠∅两种情况进行讨论,根据集合包含关系的判断和应用,分别求出满足条件的m值,并写成集合的形式即可得到答案.
解答 解:∵N⊆M,N=(x|mx=1},
当m=0,mx=1无解,故N=∅,满足条件
若N≠∅,则N={3},或N={-$\frac{1}{2}$},
∴3m=1或(-$\frac{1}{2}$)m=1.
即m=$\frac{1}{3}$,或m=-2
故满足条件的实数m∈{0,$\frac{1}{3}$,-2}.
故选:C.
点评 本题考查的知识点是集合的包含关系判断及应用,本题有两个易错点,一是忽略N=∅的情况,二是忽略题目要求满足条件的实数m的取值集合,而把答案没用集合形式表示.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
1.已知x2+y2=a2(a>0),则|xy|的最大值为( )
| A. | a2 | B. | $\frac{{a}^{2}}{2}$ | C. | $\frac{{a}^{2}}{4}$ | D. | $\frac{\sqrt{2}{a}^{2}}{2}$ |
3.函数y=|x|-2cosx的图象大致是( )
| A. | 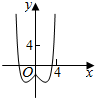 | B. | 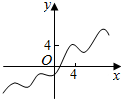 | C. | 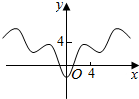 | D. | 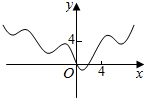 |