题目内容
设f(x)=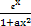 ,其中a为正实数.
,其中a为正实数.
(1)当a= 时,求f(x)的极值点.
时,求f(x)的极值点.
(2)若f(x)为[ ,
, ]上的单调函数,求a的取值范围.
]上的单调函数,求a的取值范围.
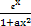 ,其中a为正实数.
,其中a为正实数.(1)当a=
 时,求f(x)的极值点.
时,求f(x)的极值点.(2)若f(x)为[
 ,
, ]上的单调函数,求a的取值范围.
]上的单调函数,求a的取值范围.(1) x1= 是极大值点,x2=
是极大值点,x2= 是极小值点 (2) 0<a≤1或a≥
是极小值点 (2) 0<a≤1或a≥
 是极大值点,x2=
是极大值点,x2= 是极小值点 (2) 0<a≤1或a≥
是极小值点 (2) 0<a≤1或a≥
f'(x)=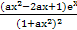 .
.
(1)当a= 时,若f'(x)=0,则4x2-8x+3=0
时,若f'(x)=0,则4x2-8x+3=0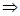 x1=
x1= ,x2=
,x2= ,则
,则
∴x1= 是极大值点,x2=
是极大值点,x2= 是极小值点.
是极小值点.
(2)记g(x)=ax2-2ax+1,则
g(x)=a(x-1)2+1-a,
∵f(x)为[ ,
, ]上的单调函数,
]上的单调函数,
则f'(x)在[ ,
, ]上不变号,
]上不变号,
∵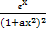 >0,
>0,
∴g(x)≥0或g(x)≤0对x∈[ ,
, ]恒成立,
]恒成立,
又g(x)的对称轴为x=1,故g(x)的最小值为g(1),最大值为g( ).
).
由g(1)≥0或g( )≤0
)≤0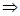 0<a≤1或a≥
0<a≤1或a≥ ,
,
∴a的取值范围是0<a≤1或a≥ .
.
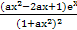 .
.(1)当a=
 时,若f'(x)=0,则4x2-8x+3=0
时,若f'(x)=0,则4x2-8x+3=0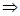 x1=
x1= ,x2=
,x2= ,则
,则| x | (-∞, ) ) |  | ( , , ) ) |  | ( ,+∞) ,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
 是极大值点,x2=
是极大值点,x2= 是极小值点.
是极小值点.(2)记g(x)=ax2-2ax+1,则
g(x)=a(x-1)2+1-a,
∵f(x)为[
 ,
, ]上的单调函数,
]上的单调函数,则f'(x)在[
 ,
, ]上不变号,
]上不变号,∵
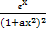 >0,
>0,∴g(x)≥0或g(x)≤0对x∈[
 ,
, ]恒成立,
]恒成立,又g(x)的对称轴为x=1,故g(x)的最小值为g(1),最大值为g(
 ).
).由g(1)≥0或g(
 )≤0
)≤0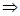 0<a≤1或a≥
0<a≤1或a≥ ,
,∴a的取值范围是0<a≤1或a≥
 .
.
练习册系列答案
相关题目
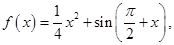
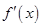 为
为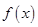 的导函数,则
的导函数,则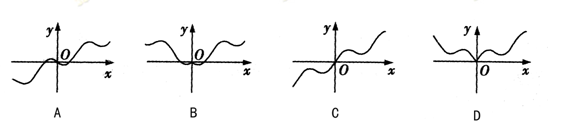
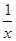 -1.
-1. x+3垂直,求切点坐标与切线的方程.
x+3垂直,求切点坐标与切线的方程. 在区间
在区间 上有极值点,则实数
上有极值点,则实数 的取值范围是( )
的取值范围是( )


