��Ŀ����
������ij�ﻧ�����콨���õ�ƽ��ʾ��ͼ��ͼ��ʾ�����滮����ȷ������Ĺ滮�����õ������ǰ뾶ΪR��Բ�森��Բ����ڽ��ı���ABCD��ԭ�ﻧ�����õأ�������֪�߽�AB =" AD" = 4���ף�BC = 6���ף�CD = 2���ף�

��1�������ԭ�ﻧ�������õ�ABCD�������Բ��İ뾶R��ֵ��
��2����������������ƣ��߽�AD��DC���ܱ�������߽�AB��BC���Ե�����Ϊ������ﻧ�����콨���õص������ʣ�����Բ��ABC�����һ��P��ʹ���ﻧ��������½����õ�APCD�������������ֵ��

��1�������ԭ�ﻧ�������õ�ABCD�������Բ��İ뾶R��ֵ��
��2����������������ƣ��߽�AD��DC���ܱ�������߽�AB��BC���Ե�����Ϊ������ﻧ�����콨���õص������ʣ�����Բ��ABC�����һ��P��ʹ���ﻧ��������½����õ�APCD�������������ֵ��
��1��S�ı���ABCD =
 ����ƽ���ף�
����ƽ���ף� �����ף�
�����ף�������������Ϊ
 ��ƽ����
��ƽ�����⣺(1)  �������Ҷ����ã�
�������Ҷ����ã�

��
��
�� ��
��
S�ı���ABCD = ����ƽ���ף�
����ƽ���ף�

��
�����Ҷ����ã� �����ף�
�����ף� �����ף� 6��
�����ף� 6��
(2) S�ı���APCD = ����
����
��AP = x��CP = y����
�����Ҷ����ã�

�� �����ҽ���x = yʱȡ������
�����ҽ���x = yʱȡ������
�� S�ı���APCD = ����ƽ���ף�
����ƽ���ף�
����AC�Ĵ�ֱƽ������Բ��ABC�Ľ��㼴Ϊ��P��
������Ϊ ��ƽ���� 12��
��ƽ���� 12��
 �������Ҷ����ã�
�������Ҷ����ã�
��

��

��
 ��
��
S�ı���ABCD =
 ����ƽ���ף�
����ƽ���ף�
��

�����Ҷ����ã�
 �����ף�
�����ף� �����ף� 6��
�����ף� 6��(2) S�ı���APCD =
 ����
����
��AP = x��CP = y����

�����Ҷ����ã�


��
 �����ҽ���x = yʱȡ������
�����ҽ���x = yʱȡ�������� S�ı���APCD =
 ����ƽ���ף�
����ƽ���ף�����AC�Ĵ�ֱƽ������Բ��ABC�Ľ��㼴Ϊ��P��
������Ϊ
 ��ƽ���� 12��
��ƽ���� 12��
��ϰ��ϵ�д�
 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
�����Ŀ
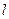 ��
��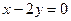 �ľ���Ϊ
�ľ���Ϊ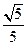 ��
��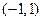 ��ֱ���ܷ���ԲC���У������У������߷��̣��������У�˵�����ɣ�
��ֱ���ܷ���ԲC���У������У������߷��̣��������У�˵�����ɣ� �������Ϊ��ʹ��������о��ͭ����ʡ������ʮ�������Բ�ܳ���̣�Ӧ������ ��ʮ���εij��Ϳ���
�������Ϊ��ʹ��������о��ͭ����ʡ������ʮ�������Բ�ܳ���̣�Ӧ������ ��ʮ���εij��Ϳ��� ����EF�ij���
����EF�ij���
 ��Բ�ĵ�ֱ��
��Բ�ĵ�ֱ�� �ľ���Ϊ2 ����
�ľ���Ϊ2 ����
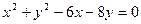 �����Բ����
�����Բ����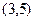 ����Һ�����ҷֱ�Ϊ
����Һ�����ҷֱ�Ϊ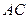 ��
��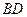 �����ı���
�����ı��� �����Ϊ �� ��
�����Ϊ �� ��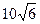
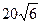
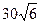
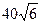
 �����EFDΪ____ _�ȣ�3�֣����߶�FD�ij�Ϊ___ ___��2�֣���
�����EFDΪ____ _�ȣ�3�֣����߶�FD�ij�Ϊ___ ___��2�֣���
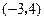 ΪԲ�ģ�����
ΪԲ�ģ�����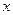 �����е�Բ�ķ����ǣ�������
�����е�Բ�ķ����ǣ�������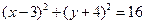

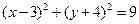
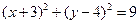
 ��Բ�������ǣ� ��
��Բ�������ǣ� �� �� B ��1��
�� B ��1�� ��
�� ��
��