题目内容
已知函数
，（1）判断函数
的单调性，并证明；（2）求函数的最小值和最大值。
（1）设
，则
∴ 
∴ 
∴ 
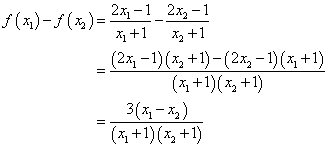
上是增函数
（2）由（1）可知上是增函数，
∴ 当
当
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
举一反三单元同步过关卷系列答案题目内容
已知函数，（1）判断函数的单调性，并证明；（2）求函数的最小值和最大值。
（1）设，则
∴
∴
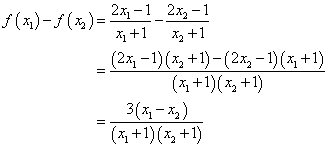
∴ 上是增函数
（2）由（1）可知上是增函数，
∴ 当
当
举一反三单元同步过关卷系列答案
，
上的单调性；
．
，求a，b的值．
．
的奇偶性；（4分）
的方程
有两解，求实数
的取值范围；（6分）
，记
，试求函数
在区间
上的最大值.（10分）
．
，
的奇偶性；（2）求证：方程
至少有一根在区间