题目内容
21.(本小题满分14分)
设 是数列
是数列 的前
的前 项和,且
项和,且 是
是 和
和 的等差中项.
的等差中项.
(1)求数列 的通项公式;
的通项公式;
(2)当 (
( 均为正整数)时,求
均为正整数)时,求 和
和 的所有可能的乘积
的所有可能的乘积 之和
之和 ;
;
(3)设 ,求证:
,求证: .
.
设
 是数列
是数列 的前
的前 项和,且
项和,且 是
是 和
和 的等差中项.
的等差中项.(1)求数列
 的通项公式;
的通项公式;(2)当
 (
( 均为正整数)时,求
均为正整数)时,求 和
和 的所有可能的乘积
的所有可能的乘积 之和
之和 ;
;(3)设
 ,求证:
,求证: .
. ,
,
21.(本小题满分14分)
(考查等差数列、等比数列、不等式的证明、数列的求和等知识,考查推理论证能力和运算求解能力和化归转化数学思想)
解:(1)∵ 是
是 和
和 的等差中项,
的等差中项,
∴ , ① ………
, ① ……… 分
分
当 时,
时, ,解得
,解得 .
.
当 时,
时,

 . ②
. ②
①-②得
 ,
,
∴ ,
,
∴ ,
,
∴
 .
.
 ∴数列
∴数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列,
∴
 . …………
. ………… 分
分
(2)由 和
和 的所有可能乘积
的所有可能乘积
 可构成下表:
可构成下表:
 ,
, ,
, ,…,
,…, ,
,
 ,
, ,…,
,…, ,
,
 ,…,
,…, ,
,
………………
 ……
…… 分
分
构造如下 行
行 列的数表:
列的数表:
 ,
, ,
, ,…,
,…, ,
,
 ,
, ,
, ,…,
,…, ,
,
 ,
, ,
, ,…,
,…, ,
,
………………
 ,
, ,
, ,… ,
,… , ,
,
设上表第一行的和为 ,则
,则
 .
.
于是

 .
.
∴ . …………
. ………… 分
分
(3)∵ ,
,
 ∴
∴ , …………
, ………… 分
分
∴

 .
.
∵ ,
,
∴ .
.
即 . …………
. ………… 分
分
(考查等差数列、等比数列、不等式的证明、数列的求和等知识,考查推理论证能力和运算求解能力和化归转化数学思想)
解:(1)∵
 是
是 和
和 的等差中项,
的等差中项,∴
 , ① ………
, ① ……… 分
分当
 时,
时, ,解得
,解得 .
.当
 时,
时,
 . ②
. ②①-②得

 ,
,∴
 ,
,∴
 ,
,∴

 .
. ∴数列
∴数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列,∴

 . …………
. ………… 分
分(2)由
 和
和 的所有可能乘积
的所有可能乘积
 可构成下表:
可构成下表: ,
, ,
, ,…,
,…, ,
,
 ,
, ,…,
,…, ,
,
 ,…,
,…, ,
,
………………
 ……
…… 分
分构造如下
 行
行 列的数表:
列的数表: ,
, ,
, ,…,
,…, ,
,
 ,
, ,
, ,…,
,…, ,
,
 ,
, ,
, ,…,
,…, ,
,
………………
 ,
, ,
, ,… ,
,… , ,
,
设上表第一行的和为
 ,则
,则 .
.于是


 .
.∴
 . …………
. ………… 分
分(3)∵
 ,
, ∴
∴ , …………
, ………… 分
分∴


 .
.∵
 ,
,∴
 .
.即
 . …………
. ………… 分
分
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
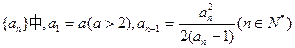
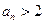 ;
;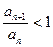 ;
;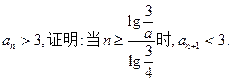
 前
前 项和为
项和为 ,若
,若 ,则
,则 ( )
( )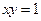 ,过
,过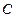 上一点
上一点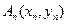 作一斜率为
作一斜率为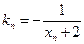 的直线交曲线C于另一点
的直线交曲线C于另一点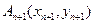 ,点
,点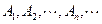 的横坐标构成数列
的横坐标构成数列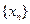 ,其中
,其中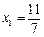 .
.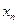 与
与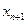 的关系式;
的关系式;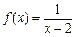 ,
,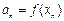 ,求
,求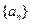 的通项公式;
的通项公式;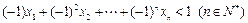 .
.
 的通项公式;
的通项公式;
 }中,
}中,  ,
, ,求
,求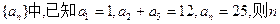 为 ( )
为 ( ) 前
前 项和为
项和为 且
且 已知
已知 则
则 ( )
( ) 中,
中, ,对所有的正整数
,对所有的正整数 ,都有
,都有 ,则
,则 等于( )
等于( ) .
.
 .
.
 .
.
 .
.