题目内容
设圆F以抛物线P:y2=4x的焦点F为圆心,且与抛物线P有且只有一个公共点.
(I)求圆F的方程;
(Ⅱ)过点M (-1,0)作圆F的两条切线与抛物线P分别交于点A,B和C,D,求经过A,B,C,D四点的圆E的方程.
(I)求圆F的方程;
(Ⅱ)过点M (-1,0)作圆F的两条切线与抛物线P分别交于点A,B和C,D,求经过A,B,C,D四点的圆E的方程.
分析:(I)设出圆F的方程,利用圆与抛物线P有且只有一个公共点,求出圆的半径,即可得到圆的方程;
(Ⅱ)设过点M(-1,0)与圆F相切的斜率为正的一条切线的切点为T,连接TF,推出∠TMF=30°,通过直线MT与抛物线的两个交点为A(x1,y1)、B(x2,y2),利用韦达定理求解|AB|,点E到直线AB的距离,求出圆E的半径R,即可求出圆E的方程.
(Ⅱ)设过点M(-1,0)与圆F相切的斜率为正的一条切线的切点为T,连接TF,推出∠TMF=30°,通过直线MT与抛物线的两个交点为A(x1,y1)、B(x2,y2),利用韦达定理求解|AB|,点E到直线AB的距离,求出圆E的半径R,即可求出圆E的方程.
解答: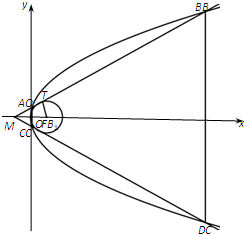 解:(Ⅰ)设圆F的方程为(x-1)2+y2=r2(r>0).
解:(Ⅰ)设圆F的方程为(x-1)2+y2=r2(r>0).
将y2=4x代入圆方程,得(x+1)2=r2,所以x=-1-r(舍去),或x=-1+r.
圆与抛物线有且只有一个公共点,
当且仅当-1+r=0,即r=1.
故所求圆F的方程为:(x-1)2+y2=1.…(4分)
(Ⅱ)设过点M(-1,0)与圆F相切的斜率为正的一条切线的切点为T.
连接TF,则TF⊥MF,且TF=1,MF=2,所以∠TMF=30°.…(6分)
直线MT的方程为x=
y-1,与y2=4x联立,得y2-4
y+4=0.
记直线与抛物线的两个交点为A(x1,y1)、B(x2,y2),则
y1+y2=4
,y1y2=4,x1+x2=
(y1+y2)-2=10.…(8分)
从而AB的垂直平分线的方程为y-2
=-
(x-5).
令y=0得,x=7.由圆与抛物线的对称性可知圆E的圆心为E(7,0).…(10分)
|AB|=
=
=8
.
又点E到直线AB的距离d=
=4,所以圆E的半径R=
=4
.
因此圆E的方程为(x-7)2+y2=48.…(12分)
 解:(Ⅰ)设圆F的方程为(x-1)2+y2=r2(r>0).
解:(Ⅰ)设圆F的方程为(x-1)2+y2=r2(r>0).将y2=4x代入圆方程,得(x+1)2=r2,所以x=-1-r(舍去),或x=-1+r.
圆与抛物线有且只有一个公共点,
当且仅当-1+r=0,即r=1.
故所求圆F的方程为:(x-1)2+y2=1.…(4分)
(Ⅱ)设过点M(-1,0)与圆F相切的斜率为正的一条切线的切点为T.
连接TF,则TF⊥MF,且TF=1,MF=2,所以∠TMF=30°.…(6分)
直线MT的方程为x=
| 3 |
| 3 |
记直线与抛物线的两个交点为A(x1,y1)、B(x2,y2),则
y1+y2=4
| 3 |
| 3 |
从而AB的垂直平分线的方程为y-2
| 3 |
| 3 |
令y=0得,x=7.由圆与抛物线的对称性可知圆E的圆心为E(7,0).…(10分)
|AB|=
| (x1-x2)2+(y1-y2)2 |
| (1+3)[(y1+y2)2-4y1y2] |
| 2 |
又点E到直线AB的距离d=
| 7-0+1 |
| 2 |
(4
|
| 3 |
因此圆E的方程为(x-7)2+y2=48.…(12分)
点评:本题考查圆的方程的求法,圆与抛物线的位置关系,点到直线的距离公式的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
 己知点F为抛物线C:y2=x的焦点,斜率为1的直线l交抛物线于不同两点P,Q.以F为圆心,以FP,FQ为半径作圆,分别交x轴负半轴于M,N,直线PM,QN交于点T.
己知点F为抛物线C:y2=x的焦点,斜率为1的直线l交抛物线于不同两点P,Q.以F为圆心,以FP,FQ为半径作圆,分别交x轴负半轴于M,N,直线PM,QN交于点T.