Question

15．如图1所示：在边长为12的正方形AA′A${\;}_{1}^{′}$A₁中，BB₁∥CC₁∥AA₁，且AB=3，BC=4，AA${\;}_{1}^{′}$分别交BB₁、CC₁于P，Q两点，将正方形沿BB₁、CC₁折叠，使得A′A${\;}_{1}^{′}$与AA₁重合，构成如图2所示的三棱柱ABC-A₁B₁C₁．
（Ⅰ）在底边AC上有一点M，且AM：MC=3：4，求证：BM∥平面APQ；
（Ⅱ）求直线BC与平面A₁PQ所成角的正弦值．

Answer 1

分析 （Ⅰ）过M作MN∥CQ交AQ于N，连接PN，由PB∥CQ得MN∥PB，从而四边形PBMN为平行四边形，对边平行BM∥PN，由线面平行的判定定理得BM∥平面APQ．
（Ⅱ）先求得各点的坐标，从而得出相应向量的坐标，再求出平面A₁PQ的法向量，由线面角公式求解．

解答 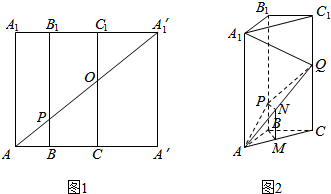（Ⅰ）证明：过M作MN∥CQ交AQ于N，连接PN，
∵AM：MC=3：4，
∴AM：AC=MN：CQ=3：7
∴MN=PB=3，
∵PB∥CQ，
∴MN∥PB，
∴四边形PBMN为平行四边形，
∴BM∥PN，
∴BM∥平面APQ，
∴BM∥平面APQ；
（Ⅱ）解：由图1知，PB=AB=3，QC=7，分别以BA，BC，BB₁为x，y，z轴，则A₁（3，0，12），C（0，4，0），P（0，0，3），Q（0，4，7）
$\overrightarrow{BC}$=（0，4，0），$\overrightarrow{{A}_{1}P}$=（-3，0，-9），$\overrightarrow{{A}_{1}Q}$=（-3，4，-5）
设平面A₁PQ的法向量为$\overrightarrow{n}$=（a，b，c），
得$\left\{\begin{array}{l}{-3a-9c=0}\\{-3a+4b-5c=0}\end{array}\right.$，
令a=-3，则c=1，b=-1，∴$\overrightarrow{n}$=（-3，-1，1）
∴cos＜$\overrightarrow{BC}$，$\overrightarrow{n}$＞=$\frac{4}{\sqrt{9+1+1}•4}$=$\frac{\sqrt{11}}{11}$
∴直线BC与平面A₁PQ所成角的正弦值为$\frac{\sqrt{11}}{11}$．

点评 本题主要考查线与线，线与面，面与面的位置关系和线面平行的判定定理及空间向量的应用，培养学生转化的能力．