题目内容
4.已知函数f(x),若在定义域内存在x0,使得f(-x0)=-f(x0)成立,则称x0为函数f(x)的局部对称点.(1)若a,b,c∈R,证明函数f(x)=ax3+bx2+cx-b必有局部对称点;
(2)是否存在常数m,使得定义在区间[-1,2]上的函数f(x)=4x+2x+m有局部对称点?若存在,求出m的范围,否则说明理由.
分析 (1)根据定义构造方程,再判断方程是否有解,问题得以解决.
(2)根据定义构造方程4x+4-x+2x+2-x+2m=0…(*)在R上有解,再利用换元法,设t=2x+2-x,方程在区间[-1,2]内有解,再根据二次函数的最值求出m的范围即可.
解答 解:(1)证明:由f(x)=ax3+bx2+cx-b得f(-x)=-ax3+bx2-cx-b,
代入f(-x)=-f(x) 得ax3+bx2+cx-b-ax3+bx2-cx-b=0得到关于x的方程2bx2-2b=0,b≠0时,x=±1
当b=0,x∈R等式恒成立,
所以函数f(x)=ax3+bx2+cx-b必有局部对称点;
(2)∵f(x)=4x+2x+m
当f(-x)=4-x+2-x+m时,f(-x)=-f(x)可化为4x+4-x+2x+2-x+2m=0,
因为f(x)的定义域为[-1,2],所以方程4x+4-x+2x+2-x+2m=0在[-1,2]上有解.
令t=2x+2-x∈[$\frac{5}{2}$,$\frac{17}{4}$],则2-2m=t2+t.t∈$[\frac{5}{2},\frac{17}{4}]$,
$\frac{9}{4}$-2m=t2+t+$\frac{1}{4}$=(t+$\frac{1}{2}$)2∈$[9,\frac{361}{16}]$,
解得m∈$[-\frac{325}{32},-\frac{27}{8}]$.
点评 本题依据新定义,考查了方程的解得问题以及参数的取值范围,以及换元的思想,转化思想,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.有4名优秀的大学毕业生被某公司录用,该公司共有5个部门,由公司人事部分安排他们去其中任意3各部门上班,每个部门至少安排一人,则不同的安排方法为( )
| A. | 120 | B. | 240 | C. | 360 | D. | 480 |
9.若1<x1<x2<3,则( )
| A. | x1lnx2<x2lnx1 | B. | x1lnx2>x2lnx1 | ||
| C. | x1e${\;}^{{x}_{2}}$<x2e${\;}^{{x}_{1}}$ | D. | x1e${\;}^{{x}_{2}}$>x2e${\;}^{{x}_{1}}$ |
16.某几何体的三视图如图所示,则该几何体的体积为( )
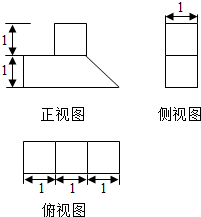

| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |