题目内容
19.实数x、y满足$\left\{\begin{array}{l}{x-y+1≤0}\\{x>0}\\{y≤2}\end{array}\right.$,若z=x2+y2,则z的取值范围是[1,5].分析 由约束条件作出可行域,然后利用z=x2+y2的几何意义,即可行域内的动点与原点距离的平方求得答案.
解答  解:由约束条件$\left\{\begin{array}{l}{x-y+1≤0}\\{x>0}\\{y≤2}\end{array}\right.$作出可行域如图,
解:由约束条件$\left\{\begin{array}{l}{x-y+1≤0}\\{x>0}\\{y≤2}\end{array}\right.$作出可行域如图,
A(0,1),
联立$\left\{\begin{array}{l}{y=2}\\{x-y+1=0}\end{array}\right.$,解得B(1,2),
z=x2+y2的几何意义为可行域内的动点与原点距离的平方,
∵|OA|=1,|OB|=$\sqrt{{1}^{2}+{2}^{2}}=\sqrt{5}$,
∴zmin=1,zmax=5.
故答案为:[1,5].
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
9.设m∈R,函数f(x)=(x-m)2+(e2x-2m)2,若存在x0使得f(x0)≤$\frac{1}{5}$成立,则m=( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
10.若△ABC的面积为64,边AB与AC的等比中项为12,则sinA=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{8}{9}$ |
3.已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{3}$=1(a>0)过点(-2,0),则双曲线的离心率为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
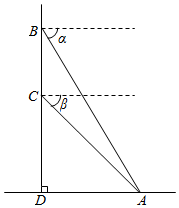 如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60m,则山高为30($\sqrt{3}$+1).
如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60m,则山高为30($\sqrt{3}$+1).