Question

【题目】已知正四棱柱的底面边长为2，侧棱，为上底面上的动点，给出下列四个结论中正确结论为（ ）

A.若，则满足条件的点有且只有一个

B.若，则点的轨迹是一段圆弧

C.若∥平面，则长的最小值为2

D.若∥平面，且，则平面截正四棱柱的外接球所得平面图形的面积为

Answer 1

【答案】ABD

【解析】

若，由于与重合时，此时点唯一；，则，即点的轨迹是一段圆弧；当为中点时，DP有最小值为，可判断C；平面截正四棱柱的外接球所得平面图形为外接球的大圆，其半径为，可得D.

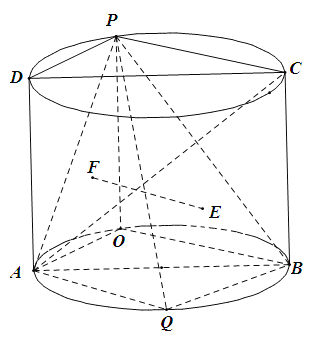
如图：

∵正四棱柱的底面边长为2，

∴，又侧棱，

∴，则与重合时，此时点唯一，故A正确；

∵，，则，即点的轨迹是一段圆弧，故B正确；

连接，，可得平面平面，则当为中点时，DP有最小值为，故C错误；

由C知，平面即为平面，平面截正四棱柱的外接球所得平面图形为外接球的大圆，其半径为，面积为，故D正确．

故选：ABD．