题目内容
【题目】已知![]() 在椭圆
在椭圆![]() 上,
上,![]() 为右焦点,
为右焦点,![]() 轴,
轴,![]() 为椭圆上的四个动点,且
为椭圆上的四个动点,且![]() ,
,![]() 交于原点
交于原点![]() .
.
(1)判断直线![]() 与椭圆的位置关系;
与椭圆的位置关系;
(2设![]() ,
,![]() 满足
满足![]() ,判断
,判断![]() 的值是否为定值,若是,请求出此定值,并求出四边形
的值是否为定值,若是,请求出此定值,并求出四边形![]() 面积的最大值,否则说明理由.
面积的最大值,否则说明理由.
【答案】(1)直线![]() 与椭圆相切或相交.(2)
与椭圆相切或相交.(2)![]() 的值是定值,
的值是定值,![]() ;
;![]()
【解析】
(1)将直线![]() 变形,可确定直线
变形,可确定直线![]() 所过定点的坐标,可得该定点坐标在椭圆上,即可判断出直线
所过定点的坐标,可得该定点坐标在椭圆上,即可判断出直线![]() 与椭圆的位置关系.
与椭圆的位置关系.
(2)先根据条件,求得椭圆的标准方程.讨论直线![]() 的斜率情况可知当斜率不存在或斜率为0时不满足
的斜率情况可知当斜率不存在或斜率为0时不满足![]() .进而设直线
.进而设直线![]() 的方程为
的方程为![]() ,联立椭圆方程,利用韦达定理及等式
,联立椭圆方程,利用韦达定理及等式![]() ,化简即可求得
,化简即可求得![]() 的值,确定
的值,确定![]() 为定值;由点到直线距离公式求得
为定值;由点到直线距离公式求得![]() ,利用弦长公式求得
,利用弦长公式求得![]() ,即可用
,即可用![]() 表示出
表示出![]() ,由二次函数性质求得
,由二次函数性质求得![]() 的最大值,并根据
的最大值,并根据![]() 即可求得
即可求得![]() 的最大值.
的最大值.
(1)直线![]() ,
,
将直线方程化简变形可得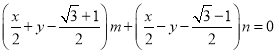 ,
,
因为![]() ,令
,令 ,解得
,解得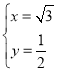 ,
,
所以直线![]() 过定点
过定点![]() ,
,
而由![]() 在椭圆上,可知直线
在椭圆上,可知直线![]() 与椭圆相切或相交.
与椭圆相切或相交.
(2)![]() 在椭圆
在椭圆![]() 上,
上,![]() 轴,
轴,
由椭圆性质可得![]() ,
,
则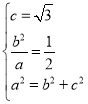 解得
解得![]() ,
,
所以椭圆的标准方程为![]() ,
,
因为![]() ,
,![]() ,
,![]() 为椭圆上的四个动点且
为椭圆上的四个动点且![]() ,
,![]() 交于原点
交于原点![]() .
.
所以![]() ,
,![]() ,
,
当直线![]() 的斜率不存在时,不满足
的斜率不存在时,不满足![]() ,因而直线
,因而直线![]() 的斜率一定存在.
的斜率一定存在.
当直线![]() 斜率存在且为0时,不满足
斜率存在且为0时,不满足![]() ,所以直线
,所以直线![]() 的斜率一定存在且不为0.
的斜率一定存在且不为0.
设直线![]() 的方程为
的方程为![]() .
.
则 ,化简可得
,化简可得![]() ,
,
所以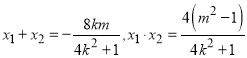 ,
,
![]()
因为![]() ,
,
所以![]() ,
,
则 ,
,
整理可得![]() ,
,
解得![]() .
.
由题意可知![]() 的位置等价,所以不妨设
的位置等价,所以不妨设![]() ,则
,则![]() ,
,
则![]() ,
,
即![]() 为定值.
为定值.
直线![]() 的方程为
的方程为![]() .即
.即![]()
则点![]() 到直线
到直线![]() 的距离为
的距离为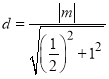
因为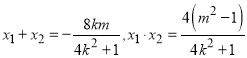
代入可得![]()
则由弦长公式可得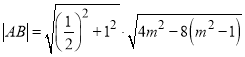
所以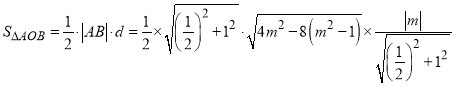
![]()
![]()
![]()
当![]() 时取等号.而
时取等号.而![]() 时满足
时满足![]() .
.
所以![]()
此时![]()
故四边形![]() 面积的最大值的最大值为4
面积的最大值的最大值为4

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
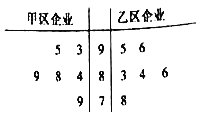
黄冈课堂作业本系列答案【题目】微信红包是一款可以实现收发红包、查收记录和提现的手机应用.某网络运营商对甲、乙两个品牌各5种型号的手机在相同环境下抢到的红包个数进行统计,得到如表数据:
手机品牌 |
|
|
|
|
|
甲品牌(个 | 4 | 3 | 8 | 6 | 12 |
乙品牌(个 | 5 | 7 | 9 | 4 | 3 |
手机品牌 | 优 | 非优 | 合计 |
| |||
乙品牌(个 | |||
合计 |
(1)如果抢到红包个数超过5个的手机型号为“优”,否则“非优”,请完成上述![]() 列联表,据此判断是否有
列联表,据此判断是否有![]() 的把握认为抢到的红包个数与手机品牌有关?
的把握认为抢到的红包个数与手机品牌有关?
(2)如果不考虑其它因素,要从甲品牌的5种型号中选出3种型号的手机进行大规模宣传销售.以![]() 表示选中的手机型号中抢到的红包超过5个的型号种数,求随机变量
表示选中的手机型号中抢到的红包超过5个的型号种数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
下面临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | <>2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]()
![]() ,其中
,其中![]() .
.