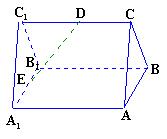
题目内容
如图,已知![]() 是正三角形,
是正三角形,![]() 都垂直于平面
都垂直于平面![]() ,且
,且![]() ,
,![]() ,
,![]() 是
是![]() 的中点,求证:
的中点,求证:
![]() (1)
(1) ![]() 平面
平面![]() ;
;
(2) ![]() 平面
平面![]() ;
;
(3) 求多面体![]() 的体积
的体积 ![]()

(3)![]()
解析:
(1)取AB的中点M,连FM,MC,
∵ F、M分别是BE、BA的中点
∴ FM∥EA, FM=![]() EA----------2分
EA----------2分
∵ EA、CD都垂直于平面ABC ∴ CD∥EA∴ CD∥FM
又 DC=a, ∴ FM=DC∴四边形FMCD是平行四边形
∴ FD∥MC ,FD∥平面ABC---------------4分
因M是AB的中点,△ABC是正三角形,所以CM⊥AB
又 CM⊥AE,所以CM⊥面EAB, CM⊥AF, FD⊥AF, --------------7分
因F是BE的中点, EA=AB所以AF⊥EB.
又因为![]() , 所以
, 所以![]() 平面
平面![]() -------------9分
-------------9分
(3)由![]() 知,
知,![]() 面
面![]() ,所以
,所以![]() 面
面![]()
所以![]() 到面
到面![]() 的距离等于
的距离等于![]() 到面
到面![]() 的距离
的距离![]() ,取
,取![]() 中点
中点![]() ,连结
,连结![]() ,
,
![]() ,则由
,则由![]() 垂直于平面
垂直于平面![]() ,知
,知![]() ,……..11分
,……..11分
故![]() 到面
到面![]() 的距离
的距离![]() ,又
,又![]() 是正三角形,所以
是正三角形,所以![]() ……12分
……12分
又由等积法知![]() ,……………….13分
,……………….13分
所以![]() …………………..14分
…………………..14分

练习册系列答案
相关题目
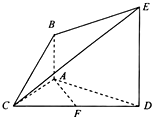 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点. 如图,已知圆锥的轴截面ABC是边长为2的正三角形,O是底面圆心.
如图,已知圆锥的轴截面ABC是边长为2的正三角形,O是底面圆心.