题目内容
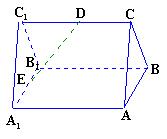
如图,已知![]() 是正三棱柱(底面为正三角形,侧棱垂直于底面),它的底面边长和侧棱长都是
是正三棱柱(底面为正三角形,侧棱垂直于底面),它的底面边长和侧棱长都是![]() .
.![]() 为侧棱
为侧棱![]() 的中点,
的中点,![]() 为底面一边
为底面一边![]() 的中点.
的中点.
(1)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(2)求证:![]() ;
;
(3)求直线![]() 到平面
到平面![]() 的距离.
的距离.
(1)![]() (2)证明见解析 (3)
(2)证明见解析 (3)![]()
解析:
(1)取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,![]() .则
.则![]()
![]()
![]() .
.

∴![]() 与
与![]() 所成的角即为
所成的角即为![]() 与
与![]() 所成的角
所成的角![]() ,
,
∵![]() 是正三棱柱,且各棱长均为
是正三棱柱,且各棱长均为![]() ,∴
,∴![]() ,
,![]() ,
,
∴△![]() 为正三角形,故
为正三角形,故![]() ,即异面直线
,即异面直线![]() 与
与![]() 所成的角为
所成的角为![]() .
.
(2)由(1)知, .
.
![]() (3)
(3) ,
,
∴点![]() 到平面
到平面![]() 的距离,即为直线
的距离,即为直线![]() 到平面
到平面![]() 的距离,由(2)易证:平面
的距离,由(2)易证:平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,则
,则![]() 为点
为点![]() 到平面
到平面![]() 的距离,由(1)知,△
的距离,由(1)知,△![]() 为正三角形且边长为
为正三角形且边长为![]() ,∴
,∴![]() ,所以直线
,所以直线![]() 到平面
到平面![]() 的距离为
的距离为![]() .w.w.w.k.s.5.u.c.o.m
.w.w.w.k.s.5.u.c.o.m

练习册系列答案
相关题目
 如图,已知ABC-A1B1C1是正三棱柱,D是AC的中点,∠C1DC=60°.
如图,已知ABC-A1B1C1是正三棱柱,D是AC的中点,∠C1DC=60°. (2013•松江区二模)如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2.
(2013•松江区二模)如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2.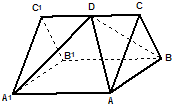 (2013•松江区二模)如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点.
(2013•松江区二模)如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点. 是正三棱柱,D是AC中点,
是正三棱柱,D是AC中点, 。
。
 (II)求异面直线
(II)求异面直线 所成的角
所成的角 为棱,
为棱, 与
与 为面的二面角的度数。
为面的二面角的度数。