题目内容
设![]() 是实数,
是实数,![]() ,
,
⑴试证明:对于任意![]() 在
在![]() 为增函数;⑵试确定
为增函数;⑵试确定![]() 的值,使
的值,使![]() 为奇函数.
为奇函数.
分析:此题虽形式较为复杂,但应严格按照单调性、奇偶性的定义进行证明。还应要求学生注意不同题型的解答方法。
⑴证明:设![]() ,则
,则
![]()
![]()
![]()
![]() ,
,
由于指数函数![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,所以
,所以![]() 即
即![]() ,
,
又由![]() ,得
,得![]() ,
,![]() ,∴
,∴![]() 即
即![]() .
.
因为此结论与![]() 取值无关,所以对于
取值无关,所以对于![]() 取任意实数,
取任意实数,![]() 在
在![]() 为增函数。
为增函数。
说明:上述证明过程中,在对差式正负判断时,利用了指数函数的值域及单调性。
⑵解:若![]() 为奇函数,则
为奇函数,则![]() ,
,
即![]() ,即:
,即:![]() ,
,
解得:![]() ,∴当
,∴当![]() 时,
时, ![]() 为奇函数。
为奇函数。
说明:此题并非直接确定![]() 值,而是由已知条件逐步推导
值,而是由已知条件逐步推导![]() 值。
值。

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
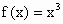 .
.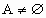 ,求实数a的取值范围.
,求实数a的取值范围.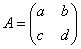 为二阶实系数方阵,
为二阶实系数方阵,