Question

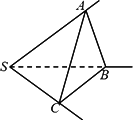
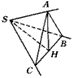
过点S引三条不共面的直线SA、SB、SC，如图，∠BSC=90°，∠ASC=∠ASB=60°，若截取SA=SB=SC=a．

(1)求证：平面ABC⊥平面BSC；

(2)求S到平面ABC的距离．

Answer 1

答案：略
解析：

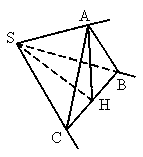
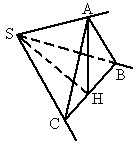
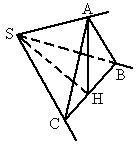
(1)证法1：∵SA=SB=SC=a， 又∠ASC=∠ASB=60°， ∴△ASB和△ASC都是等边三角形． ∴AB=AC=a． 取BC的中点为H，连结AH，则AH⊥BC． 在Rt△BSC中，BS=CS=a， ∴SH⊥BC，BC=． ∴．∴． 在△SHA中，∵， ∴．∴AH⊥SH． ∴AH⊥平面SBC． ∴AH平面ABC，∴平面ABC⊥平面SBC． 证法2：∵SA=AC=AB， ∴顶点A在平面BSC内的射影H为△BSC的外心． 又△BSC为直角三角形，∴H在斜边BC上． 又△BSC为等腰直角三角形， ∴H为BC的中点． ∴AH⊥平面BSC． ∵AH平面ABC，∴平面ABC⊥平面BSC． (2)解：由前所证：SH⊥AH，SH⊥BC，∴SH⊥平面ABC． ∴的长即为点S到平ABC有距离．又， ∴点S到平面ABC的距离为．

提示：

要证明平面ABC⊥平面BSC，根据面面垂直的判定定理，需在平面ABC或平面BSC内找到一条与另一个平面垂直的直线．