Question

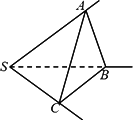
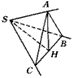
过点S引三条不共面的直线SA、SB、SC，如图，∠BSC=90°，∠ASC=∠ASB=60°，若截取SA=SB=SC=a，
（1）求证：平面ABC⊥平面BSC；
（2）求S到平面ABC的距离．

Answer 1

（1）证明：∵SA=SB=SC=a，
又∠ASC=∠ASB=60°，
∴△ASB和△ASC都是等边三角形，
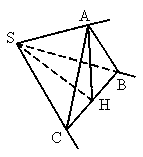
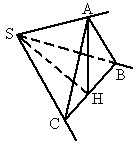
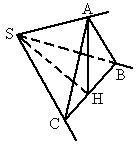
∴AB=AC=a，取BC的中点H，连结AH，
∴AH⊥BC，
在Rt△BSC中，BS=CS=a，
∴SH⊥BC，，
∴，
∴，
在△SHA中，∴，，，
∴，∴AH⊥SH，
∴AH⊥平面SBC，
∵AH平面ABC，
∴平面ABC⊥平面BSC。
（2）解：由前所证：SH⊥AH，SH⊥BC，∴SH⊥平面ABC，
∴SH的长即为点S到平面ABC的距离，，
∴点S到平面ABC的距离为．