题目内容
在边长为a的等边三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,
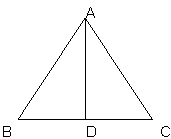 BC=a,这时二面角B-AD-C的大小为
BC=a,这时二面角B-AD-C的大小为
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
题目内容
在边长为a的等边三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,
 BC=a,这时二面角B-AD-C的大小为
BC=a,这时二面角B-AD-C的大小为
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案