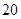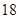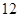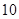题目内容
已知椭圆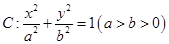 的一个焦点为
的一个焦点为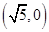 ,离心率为
,离心率为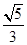 .
.
(1)求椭圆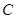 的标准方程;
的标准方程;
(2)若动点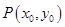 为椭圆
为椭圆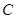 外一点,且点
外一点,且点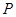 到椭圆
到椭圆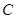 的两条切线相互垂直,求点
的两条切线相互垂直,求点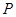 的轨迹方程.
的轨迹方程.
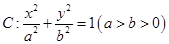 的一个焦点为
的一个焦点为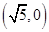 ,离心率为
,离心率为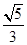 .
.(1)求椭圆
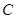 的标准方程;
的标准方程;(2)若动点
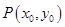 为椭圆
为椭圆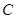 外一点,且点
外一点,且点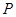 到椭圆
到椭圆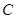 的两条切线相互垂直,求点
的两条切线相互垂直,求点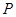 的轨迹方程.
的轨迹方程.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)利用题中条件求出
 的值,然后根据离心率求出
的值,然后根据离心率求出 的值,最后根据
的值,最后根据 、
、 、
、 三者的关系求出
三者的关系求出 的值,从而确定椭圆
的值,从而确定椭圆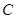 的标准方程;(2)分两种情况进行计算:第一种是在从点
的标准方程;(2)分两种情况进行计算:第一种是在从点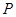 所引的两条切线的斜率都存在的前提下,设两条切线的斜率分别为
所引的两条切线的斜率都存在的前提下,设两条切线的斜率分别为 、
、 ,并由两条切线的垂直关系得到
,并由两条切线的垂直关系得到 ,并设从点
,并设从点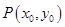 所引的直线方程为
所引的直线方程为 ,将此直线的方程与椭圆的方程联立得到关于
,将此直线的方程与椭圆的方程联立得到关于 的一元二次方程,利用
的一元二次方程,利用 得到有关
得到有关 的一元二次方程,最后利用
的一元二次方程,最后利用 以及韦达定理得到点
以及韦达定理得到点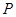 的轨迹方程;第二种情况是两条切线与坐标轴垂直的情况下求出点
的轨迹方程;第二种情况是两条切线与坐标轴垂直的情况下求出点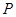 的坐标,并验证点
的坐标,并验证点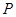 是否在第一种情况下所得到的轨迹上,从而得到点
是否在第一种情况下所得到的轨迹上,从而得到点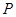 的轨迹方程.
的轨迹方程.(1)由题意知
 ,且有
,且有 ,即
,即 ,解得
,解得 ,
,因此椭圆
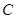 的标准方程为
的标准方程为 ;
;(2)①设从点
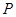 所引的直线的方程为
所引的直线的方程为 ,即
,即 ,
,当从点
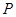 所引的椭圆
所引的椭圆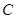 的两条切线的斜率都存在时,分别设为
的两条切线的斜率都存在时,分别设为 、
、 ,则
,则 ,
,将直线
 的方程代入椭圆
的方程代入椭圆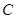 的方程并化简得
的方程并化简得 ,
, ,
,化简得
 ,即
,即 ,
,则
 、
、 是关于
是关于 的一元二次方程
的一元二次方程 的两根,则
的两根,则 ,
,化简得
 ;
;②当从点
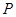 所引的两条切线均与坐标轴垂直,则
所引的两条切线均与坐标轴垂直,则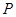 的坐标为
的坐标为 ,此时点
,此时点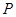 也在圆
也在圆 上.
上.综上所述,点
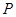 的轨迹方程为
的轨迹方程为 .
. 的符号来进行转化,计算量较大,从中也涉及了方程思想的灵活应用,属于难题.
的符号来进行转化,计算量较大,从中也涉及了方程思想的灵活应用,属于难题.
练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 上;
上;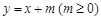 与椭圆W:
与椭圆W: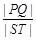 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.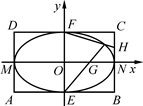
 的左、右焦点分别为
的左、右焦点分别为 ,,右顶点为A,上顶点为B.已知
,,右顶点为A,上顶点为B.已知 =
=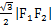 .
. ,经过点
,经过点 的直线
的直线 与该圆相切与点M,
与该圆相切与点M, =
= .求椭圆的方程.
.求椭圆的方程.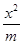 +
+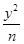 =1与双曲线
=1与双曲线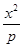 -
-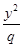 =1(m,n,p,q均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则
=1(m,n,p,q均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则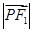 ·
·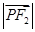 =( )
=( )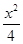 +
+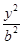 =1(b>0),直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
=1(b>0),直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )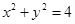 的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线
的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线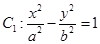 过点P且离心率为
过点P且离心率为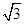 .
.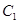 的方程;
的方程;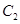 过点P且与
过点P且与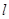 过
过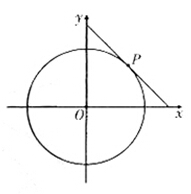
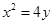 的准线与椭圆
的准线与椭圆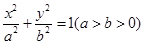 相切,且该切点与椭圆的两焦点构成的三角形面积为2,则椭圆的离心率是( )
相切,且该切点与椭圆的两焦点构成的三角形面积为2,则椭圆的离心率是( )



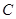 的中心在原点,焦点在
的中心在原点,焦点在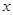 轴上,离心率为
轴上,离心率为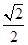 ,它的一个焦点恰好与抛物线
,它的一个焦点恰好与抛物线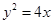 的焦点重合.
的焦点重合.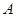 ,过点
,过点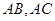 ,若直线
,若直线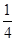 ,直线
,直线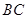 是否一定经过一定点?若经过,求出该定点坐标;若不经过,请说明理由.
是否一定经过一定点?若经过,求出该定点坐标;若不经过,请说明理由.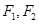 为椭圆
为椭圆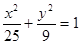 的两个焦点,过
的两个焦点,过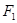 的直线交椭圆于两点,
的直线交椭圆于两点,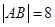 ,
,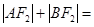 ( )
( )