题目内容
设数列
：
，求
.
解析:
设
，将
代入递推式，得
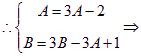
…（１）则
,又
，故
代入（１）得
说明：（1）若
为
的二次式，则可设
;(2)本题也可由
,
（
）两式相减得
转化为
求之.
练习册系列答案
出彩同步大试卷系列答案
相关题目
解析:
出彩同步大试卷系列答案题目内容
设数列：，求.
设，将代入递推式，得
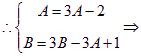
…（１）则,又，故代入（１）得
说明：（1）若为的二次式，则可设;(2)本题也可由 ,（）两式相减得转化为求之.
出彩同步大试卷系列答案
的前
项和
满足
，且
为正整数）。
满足
，求
；
，问是否存在正整数
，使得
时恒有
成立？若存在，请求出所有
过点P
斜率为
，与直线
：
交于点A，与
轴交于点B，点A，B的横坐标分别为
，记
.
的解析式；
满足
，求数列
的通项公式；
时，证明不等式：
.
满足
求数列
的前
项和
.
}中，
=3，其前
项和为
，等比数列{
}的各项均为正数，
=1，公比为q,且b2+ S2=12，
．
}满足
，求{
．
满足
，求
，
，由此猜想
的通项公式，并用数学归纳法证明你的结论。