题目内容
【题目】定义:给定整数i,如果非空集合满足如下3个条件:
①![]() ;②
;②![]() ;③
;③![]() ,若
,若![]() ,则
,则![]() .
.
则称集合A为“减i集”
(1)![]() 是否为“减0集”?是否为“减1集”?
是否为“减0集”?是否为“减1集”?
(2)证明:不存在“减2集”;
(3)是否存在“减1集”?如果存在,求出所有“减1集”;如果不存在,说明理由.
【答案】(1)是“减0集”;不是“减1集”(2)证明见解析;(3)存在;![]() ,
,![]() ,
,![]() ,3,
,3,![]() ,
,![]() ,3,5,
,3,5,![]() ,
,![]()
![]() ,3,5,
,3,5,![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)![]() ,
,![]() ,
,![]() ,
,![]() ,即可得出
,即可得出![]() 是“减0集”,同理可得
是“减0集”,同理可得![]() 不是“减1集”.
不是“减1集”.
(2)假设存在![]() 是“减2集”,则若
是“减2集”,则若![]() ,那么
,那么![]() ,当
,当![]() 时,有
时,有![]() ,对
,对![]() ,
,![]() 分类讨论即可得出.
分类讨论即可得出.
(3)存在“减1集” ![]() .
.![]() .假设
.假设![]() ,则
,则![]() 中除了元素1以外,必然还含有其它元素.假设
中除了元素1以外,必然还含有其它元素.假设![]() ,
,![]() ,而
,而![]() ,因此
,因此![]() .假设
.假设![]() ,
,![]() ,而
,而![]() ,因此
,因此![]() .因此可以有
.因此可以有![]() ,
,![]() .假设
.假设![]() ,
,![]() ,而
,而![]() ,因此
,因此![]() .假设
.假设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,因此
,因此![]() .
.
因此可以有![]() ,3,
,3,![]() .以此类推可得所有的
.以此类推可得所有的![]() .
.
(1)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是“减0集”
是“减0集”
同理,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 不是“减1集”.
不是“减1集”.
(2)假设存在![]() 是“减2集”,则若
是“减2集”,则若![]() ,
,
那么![]() ,当
,当![]() 时,有
时,有![]() ,
,
则![]() ,
,![]() 一个为2,一个为4,所以集合
一个为2,一个为4,所以集合![]() 中有元素6,
中有元素6,
但是![]() ,
,![]() ,与
,与![]() 是“减2集”,矛盾,故不存在“减2集”
是“减2集”,矛盾,故不存在“减2集”
(3)存在“减1集”![]() .
.![]() .
.
①假设![]() ,则
,则![]() 中除了元素1以外,必然还含有其它元素.
中除了元素1以外,必然还含有其它元素.
假设![]() ,
,![]() ,而
,而![]() ,因此
,因此![]() .
.
假设![]() ,
,![]() ,而
,而![]() ,因此
,因此![]() .
.
因此可以有![]() ,
,![]() .
.
假设![]() ,
,![]() ,而
,而![]() ,因此
,因此![]() .
.
假设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,因此
,因此![]() .
.
因此可以有![]() ,3,
,3,![]() .
.
以此类推可得:![]() ,3,5,
,3,5,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
以及![]() 的满足以下条件的非空子集:
的满足以下条件的非空子集:![]() ,
,![]() ,
,![]() ,3,
,3,![]() ,
,![]() ,3,5,
,3,5,![]() ,
,![]()

【题目】中国武汉于2019年10月18日至2019年10月27日成功举办了第七届世界军人运动会.来自109个国家的9300余名运动员同台竞技.经过激烈的角逐,奖牌榜的前3名如下:
国家 | 金牌 | 银牌 | 铜牌 | 奖牌总数 |
中国 | 133 | 64 | 42 | 239 |
俄罗斯 | 51 | 53 | 57 | 161 |
巴西 | 21 | 31 | 36 | 88 |
某数学爱好者采用分层抽样的方式,从中国和巴西获得金牌选手中抽取了22名获奖代表.从这22名中随机抽取3人, 则这3人中中国选手恰好1人的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【题目】某学校为了了解该校某年级学生的阅读量(分钟),随机抽取了![]() 名学生调查一天的阅读时间,统计结果如下图表所示:
名学生调查一天的阅读时间,统计结果如下图表所示:
组号 | 分组 | 男生人数 | 男生人数占本组人数的频率 | 频率分布直方图 |
第1组 |
| 5 | 0.5 |
|
第2组 |
| 18 | 0.9 | |
第3组 |
| 27 | 0.9 | |
第4组 |
|
| 0.36 | |
第5组 |
| 3 | 0.2 |
(1)求出![]() 的值并估计该校学生一天的人均阅读时间;
的值并估计该校学生一天的人均阅读时间;
(2)一天的阅读时间不少于35分钟称为“喜好阅读者”.根据以上数据,完成下面的![]() 列联表,并回答能否在犯错误的概率不超过0.05的前提下认为“喜好阅读者”与“性别”有关?
列联表,并回答能否在犯错误的概率不超过0.05的前提下认为“喜好阅读者”与“性别”有关?
喜好阅读者 | 非喜好阅读者 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: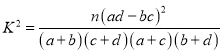 (其中
(其中![]() 为样本容量).
为样本容量).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |