题目内容
 已知向量
已知向量 =(a-2b,a),
=(a-2b,a), =(a+2b,3b),且
=(a+2b,3b),且 ,
, 的夹角为钝角,则在平面aOb上,满足上述条件及a2+b2≤1的点(a,b)所在的区域面积S满足
的夹角为钝角,则在平面aOb上,满足上述条件及a2+b2≤1的点(a,b)所在的区域面积S满足
- A.S=π
- B.S=

- C.S>

- D.S<

D
分析:先根据夹角为钝角得到 .
. <0,进而得到(a+4b)(a-b)<0,再结合图象即可得到结论.
<0,进而得到(a+4b)(a-b)<0,再结合图象即可得到结论.
解答:∵ ,
, 的夹角为钝角,
的夹角为钝角,
∴cos< ,
, >=
>= <0,
<0,
∴ •
• <0,
<0,
即(a-2b,a)•(a+2b,3b)=a2-4b2+3ab=(a+4b)(a-b)<0.
∴ 或
或 ,
,
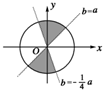
画出上述可行域及a2+b2≤1(如图).
显然直线b=a与b=- a的夹角为锐角.
a的夹角为锐角.
∴S< .
.
故应选D.
故选:D
点评:本题主要考察平面向量的数量积的应用问题.解决本题的关键在于根据夹角为钝角得到 •
• <0,进而得到(a+4b)(a-b)<0.
<0,进而得到(a+4b)(a-b)<0.
分析:先根据夹角为钝角得到
 .
. <0,进而得到(a+4b)(a-b)<0,再结合图象即可得到结论.
<0,进而得到(a+4b)(a-b)<0,再结合图象即可得到结论.解答:∵
 ,
, 的夹角为钝角,
的夹角为钝角,∴cos<
 ,
, >=
>= <0,
<0,∴
 •
• <0,
<0,即(a-2b,a)•(a+2b,3b)=a2-4b2+3ab=(a+4b)(a-b)<0.
∴
 或
或 ,
,画出上述可行域及a2+b2≤1(如图).
显然直线b=a与b=-
 a的夹角为锐角.
a的夹角为锐角.∴S<
 .
.故应选D.
故选:D
点评:本题主要考察平面向量的数量积的应用问题.解决本题的关键在于根据夹角为钝角得到
 •
• <0,进而得到(a+4b)(a-b)<0.
<0,进而得到(a+4b)(a-b)<0. 
练习册系列答案
相关题目
 已知向量
已知向量 .若a— 2b与c共线,则k=________.
.若a— 2b与c共线,则k=________. .若a— 2b与c共线,则k=________.
.若a— 2b与c共线,则k=________.



 。若a-2b与c共线,则k=( )。
。若a-2b与c共线,则k=( )。