题目内容
如图所示,已知三棱柱ABC—A1B1C1的各棱长均为2,侧棱B1B与底面ABC所成的角为(1)求证:AB⊥CB1;
(2)求三棱锥B1—ABC的体积;
(3)求二面角C—AB1—B的大小.
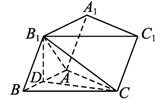
(1)证明:如图(1)在平面ABB1A1内,过B1作B1D⊥AB于D,

(1)
∵侧面ABB1A1⊥平面ABC,
∴B1D⊥平面ABC.
∴∠B1BA是B1B与底面ABC所成的角.
∴∠B1BA=60°.
∵三棱柱的各棱长均为2,
∴△ABB1是正三角形.
∴D是AB的中点.连结CD,在等边△ABC中,CD⊥AB,
∴AB⊥平面CDB1.∴AB⊥CB1.
(2)解:∵B1D⊥平面ABC,
∴B1D是三棱锥B1—ABC的高,由B1B=2,∠B1BA=60°得B1D=2sin60°=3,
∴![]() =
=![]() S△ABC·B1D
S△ABC·B1D
=![]() (
(![]() ×
×![]() ×2×2)·
×2×2)·![]() =1.
=1.
(3)解:∵△ABC是正三角形,CD⊥AB,CD⊥B1D,
∴CD⊥平面ABB1.
在平面ABB1中作DE⊥AB1于E,连结CE,由三垂线定理知CE⊥AB1,
∴∠CED为二面角C—AB1—B的平面角.在Rt△CED中,CD=2sin60°=![]() ,连结BA1交AB1于O,则BO=
,连结BA1交AB1于O,则BO=![]() .
.
∴DE=![]() BO=
BO=![]() .
.
∴tan∠CED=![]() =2.
=2.
∴所求二面角C—AB1—B的大小为arctan2.

练习册系列答案
相关题目
 如图所示,已知三棱柱ABC-A1B1C1的各棱长均为2,侧棱B1B与底面ABC所成的角为,且侧面ABB1A1垂直于底面ABC.
如图所示,已知三棱柱ABC-A1B1C1的各棱长均为2,侧棱B1B与底面ABC所成的角为,且侧面ABB1A1垂直于底面ABC. 如图所示,已知三棱柱A′B′C′-ABC的侧棱垂直于底面,AC⊥CB,且AC=CB=CC′=2.若点E为A′B′中点,则CE与底面ABC所成角的余弦值为
如图所示,已知三棱柱A′B′C′-ABC的侧棱垂直于底面,AC⊥CB,且AC=CB=CC′=2.若点E为A′B′中点,则CE与底面ABC所成角的余弦值为 如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1-ABC1的体积为( )
如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1-ABC1的体积为( ) 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 上的
上的 的中点,则异面直线
的中点,则异面直线 与
与 所成的角的余弦值为( )
所成的角的余弦值为( ) B.
B.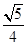 C.
C. D.
D.

 ,在某个空间直角坐标系中,
,在某个空间直角坐标系中, ,
, ,其中
,其中 、
、

 ,求直线
,求直线 与平面
与平面 所成角的大小。
所成角的大小。