题目内容
1.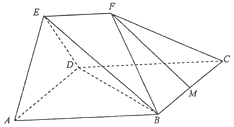 已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.
已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.(Ⅰ)求证:直线MF∥平面BED;
(Ⅱ)求平面BED与平面FBC所成角的正弦值;
(Ⅲ)求直线BF与平面BED所成角的正弦值.
分析 (Ⅰ)取BD的中点G,连结MG,EG,通过证明四边形EFMG是平行四边形得出MF∥EG,从而有MF∥平面BED;
(Ⅱ)以O为原点建立空间坐标系,求出平面BED和平面FBC的法向量,通过计算法向量的夹角得出二面角的大小;
(Ⅲ)通过计算法向量与$\overrightarrow{BF}$的夹角得出直线BF与平面BED所成角.
解答 证明:(I)取BD的中点G,连结MG,EG,
∵M为线段BC的中点,G是BD的中点,
∵MG$\stackrel{∥}{=}$$\frac{1}{2}$CD,又CD$\stackrel{∥}{=}AB$,EF$\stackrel{∥}{=}$$\frac{1}{2}$AB,
∴EF$\stackrel{∥}{=}$GM,
∴四边形EFMG是平行四边形,
∴MF∥EG,
又MF?平面BED,EG?平面BED,
∴MF∥平面BED.
解:(II)过E作EO⊥AD,垂足为O,则O为AD的中点,
∵平面AED⊥平面ABCD,平面AED∩平面ABCD=AD,OE⊥AB,OE?平面EAD,
∴OE⊥平面ABCD,
过O作ON⊥AB,垂足为N,则ON⊥OM,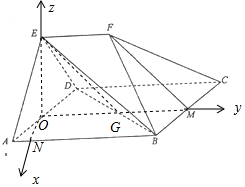
以O为原点,以ON,OM,OE为坐标轴建立空间直角坐标系,
如图所示:
则E(0,0,$\sqrt{3}$),M(0,2$\sqrt{2}$,0),G(0,$\sqrt{2}$,0),
B($\frac{\sqrt{2}}{2}$,$\frac{3\sqrt{2}}{2}$,0),F(0,$\sqrt{2}$,$\sqrt{3}$),
∴$\overrightarrow{BE}$=(-$\frac{\sqrt{2}}{2}$,-$\frac{3\sqrt{2}}{2}$,$\sqrt{3}$),$\overrightarrow{GE}$=(0,-$\sqrt{2}$,$\sqrt{3}$),
$\overrightarrow{BM}$=(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$,0),$\overrightarrow{MF}$=(0,-$\sqrt{2}$,$\sqrt{3}$).
设平面BDE的法向量为$\overrightarrow{m}$=(x1,y1,z1),
平面BCF的法向量为$\overrightarrow{n}$=(x2,y2,z2),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BE}=0}\\{\overrightarrow{m}•\overrightarrow{GE}=0}\end{array}\right.$,$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BM}=0}\\{\overrightarrow{n}•\overrightarrow{MF}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{-\frac{\sqrt{2}}{2}{x}_{1}-\frac{3\sqrt{2}}{2}{y}_{1}+\sqrt{3}{z}_{1}=0}\\{-\sqrt{2}{y}_{1}+\sqrt{3}{z}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{-\frac{\sqrt{2}}{2}{x}_{2}+\frac{\sqrt{2}}{2}{y}_{2}=0}\\{-\sqrt{2}{y}_{2}+\sqrt{3}{z}_{2}=0}\end{array}\right.$,
令y1=y2=$\sqrt{3}$得$\overrightarrow{m}$=(-$\sqrt{3}$,$\sqrt{3}$,$\sqrt{2}$),$\overrightarrow{n}$=($\sqrt{3}$,$\sqrt{3}$,$\sqrt{2}$),
∴cos<$\overrightarrow{m,}\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{2}{2\sqrt{2}×2\sqrt{2}}$=$\frac{1}{4}$,
设平面BED与平面FBC所成角为θ,则|cosθ|=$\frac{1}{4}$,∴sinθ=$\sqrt{1-co{s}^{2}θ}$=$\frac{\sqrt{15}}{4}$.
∴平面BED与平面FBC所成角的正弦值为$\frac{\sqrt{15}}{4}$.
解:(III)$\overrightarrow{BF}$=(-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$,$\sqrt{3}$),
cos<$\overrightarrow{BF},\overrightarrow{m}$>=$\frac{\overrightarrow{BF}•\overrightarrow{m}}{|\overrightarrow{BF}||\overrightarrow{m}|}$=$\frac{\sqrt{6}}{2×2\sqrt{2}}$=$\frac{\sqrt{3}}{4}$,
设直线BF与平面BED所成角为α,则sinα=|cos<$\overrightarrow{BF},\overrightarrow{m}$>|=$\frac{\sqrt{3}}{4}$.
∴直线BF与平面BED所成角的正弦值为$\frac{\sqrt{3}}{4}$.
点评 本题考查了线面平行的判定,空间向量与空间角的计算,属于中档题.

| A. | 命题“?x0∈R,2${\;}^{{x}_{0}}$>1”的否定是“?x∈R,2x≤1” | |
| B. | 命题“若x=y,则x2=y2”的否命题是“若x=y,则x2≠y2” | |
| C. | p:?x∈R,x2+1≥1,q:在△ABC中,若sinA=$\frac{1}{2}$,则A=$\frac{π}{6}$,则p∧q为真命题 | |
| D. | 若平面α⊥平面β,直线a?α,直线b?β,则a⊥b |
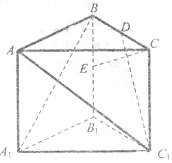 在棱长为2的正三棱柱ABC-A1B1C1中,D,E分别是BC,BB1的中点.
在棱长为2的正三棱柱ABC-A1B1C1中,D,E分别是BC,BB1的中点. ,
,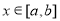 ,那么集合
,那么集合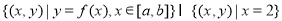 中元素的个数为( )
中元素的个数为( ) ,则不等式
,则不等式 的解集为 .
的解集为 .