题目内容
若f（x）=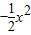
+bln（x+2）在（-1，+∞）上是减函数，求b的取值范围．
【答案】分析：求出导数f′（x），则f（x）在（-1，+∞）上是减函数等价于-x+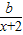
≤0在（-1，+∞）上恒成立，分离参数b后，转化为求函数最值即可，根据二次函数的性质易求函数最值．
解答：解：f′（x）=-x+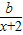
，
故f（x）在（-1，+∞）上是减函数等价于-x+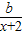
≤0在（-1，+∞）上恒成立，
由x＞-1得x+2＞0，
原命题成立等价于b≤x2+2x在（-1，+∞）上恒成立，
又y=x2+2x在（-1，+∞）上单调递增，x2+2x＞-1，
故b≤-1，
故b的取值范围为（-∞，-1]．
点评：本题考查函数的单调性与导数的关系，可导函数f（x）在（a，b）上单调递增的充要条件为f′（x）≥0．
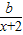≤0在（-1，+∞）上恒成立，分离参数b后，转化为求函数最值即可，根据二次函数的性质易求函数最值．解答：解：f′（x）=-x+
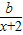，故f（x）在（-1，+∞）上是减函数等价于-x+
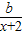≤0在（-1，+∞）上恒成立，由x＞-1得x+2＞0，
原命题成立等价于b≤x2+2x在（-1，+∞）上恒成立，
又y=x2+2x在（-1，+∞）上单调递增，x2+2x＞-1，
故b≤-1，
故b的取值范围为（-∞，-1]．
点评：本题考查函数的单调性与导数的关系，可导函数f（x）在（a，b）上单调递增的充要条件为f′（x）≥0．
练习册系列答案
相关题目
若f（x）=-
x2+bln（x+2）在（-1，+∞）上是减函数，则b的取值范围是（ ）
| 1 |
| 2 |
| A、[-1，+∞） |
| B、（-1，+∞） |
| C、（-∞，-1] |
| D、（-∞，-1） |
+bln（x+2）在（0，+∞）上是减函数，则b的取值范围是 ．