题目内容
【题目】如图,在矩形纸片![]() 中,
中,![]() ,
,![]() ,在线段
,在线段![]() 上取一点
上取一点![]() ,沿着过
,沿着过![]() 点的直线将矩形右下角折起,使得右下角顶点
点的直线将矩形右下角折起,使得右下角顶点![]() 恰好落在矩形的左边
恰好落在矩形的左边![]() 边上.设折痕所在直线与
边上.设折痕所在直线与![]() 交于
交于![]() 点,记折痕
点,记折痕![]() 的长度为
的长度为![]() ,翻折角
,翻折角![]() 为
为![]() .
.

(1)探求![]() 与
与![]() 的函数关系,推导出用
的函数关系,推导出用![]() 表示
表示![]() 的函数表达式;
的函数表达式;
(2)设![]() 的长为
的长为![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)确定点![]() 在何处时,翻折后重叠部分的图形面积最小.
在何处时,翻折后重叠部分的图形面积最小.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,翻折后重叠部分的图形面积最小
时,翻折后重叠部分的图形面积最小
【解析】
(1)由图可知![]() 与
与![]() 的函数关系式为
的函数关系式为 ![]() =
=![]() ,再求函数定义域的范围即可;
,再求函数定义域的范围即可;
(2)由三角函数的性质求函数在区间上的值域即可;
(3)由均值不等式求函数的最值,由取等的条件求出![]() 的值即可.
的值即可.
解:(1)设顶点![]() 翻折到边
翻折到边![]() 上的点为
上的点为![]() ,由题意可得
,由题意可得![]() ,
,
![]() ,因为
,因为![]() ,
,
所以![]() =
=![]() ,
,
即![]() 与
与![]() 的函数关系式为
的函数关系式为 ![]() =
=![]() ,
,
由题意有![]() ,首先利用
,首先利用![]() ,可知
,可知![]() ,
,
解得![]() ,所以
,所以![]() ,
,
又由![]() ,可知
,可知![]() ,即
,即![]() ,
,
即![]() ,
,
故![]() 与
与![]() 的函数关系式为
的函数关系式为 ![]() =
=![]() ,
,![]() ;
;
(2)![]() ,
,
当![]() ,
,![]() ,
,
所以![]() ,
,
故![]() 的取值范围为
的取值范围为![]() ;
;
(3)![]() ,
,
又![]()
![]()
(当且仅当![]() =
=![]() 即
即![]() 时取等号,
时取等号,
故当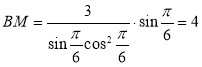 时,
时,![]() 取最小值
取最小值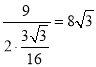 ,
,
故 ![]() 时,
时,![]() 取最小值
取最小值![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目