题目内容
【题目】已知函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)当![]() 时,
时,![]() 在定义域内恒成立,求实数
在定义域内恒成立,求实数![]() 的值.
的值.
【答案】(Ⅰ)当![]() 时,单调递增区间为
时,单调递增区间为![]() ,无单调递减区间;当
,无单调递减区间;当![]() 时,单调递增区间为
时,单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]()
(Ⅱ)![]()
【解析】
(Ⅰ)求出函数![]() 的的定义域以及导函数,分类讨论
的的定义域以及导函数,分类讨论![]() ,
,![]() ,
,![]() 情况下导数的正负,由此得到答案;
情况下导数的正负,由此得到答案;
(Ⅱ)结合(Ⅰ)可得函数![]() 的最小值,要使
的最小值,要使![]() 在定义域内恒成立,则
在定义域内恒成立,则![]() 恒成立,令
恒成立,令![]() ,利用导数求出
,利用导数求出![]() 的最值,从而得到实数
的最值,从而得到实数![]() 的值。
的值。
(Ⅰ)由题可得函数![]() 的的定义域为
的的定义域为![]() ,
,![]() ;
;
(1) 当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 单调递增区间为
单调递增区间为![]() ,无单调递减区间
,无单调递减区间
(2) 当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 单调递增区间为
单调递增区间为![]() ,无单调递减区间;
,无单调递减区间;
(3) 当![]() 时,令
时,令![]() ,解得:
,解得:![]() ,令
,令![]() ,解得:
,解得:![]() ,则
,则![]() 单调递增区间为
单调递增区间为![]() ,
,![]() 单调递减区间为
单调递减区间为![]() ;
;
综述所述:当![]() 时,单调递增区间为
时,单调递增区间为![]() ,无单调递减区间;当
,无单调递减区间;当![]() 时,单调递增区间为
时,单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(Ⅱ)由(Ⅰ)可知,当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,则
,则![]() ;
;
所以![]() 在定义域内恒成立,则
在定义域内恒成立,则![]() 恒成立,即
恒成立,即![]() ,
,
令![]() ,先求
,先求![]() 的最大值:
的最大值:![]() ,令
,令![]() ,解得:
,解得:![]() ,令
,令![]() ,解得:
,解得:![]() ,令
,令![]() ,解得:
,解得:![]() ,所以
,所以![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ,则
,则![]()
所以当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 在定义域内恒成立,
在定义域内恒成立,
故答案为![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】工厂车间某部门有8个小组,在一次技能考试中成绩情况分析如下:
小组 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
大于90分人数 | 6 | 6 | 7 | 3 | 5 | 3 | 3 | 7 |
不大于90分人数 | 39 | 39 | 38 | 42 | 40 | 42 | 42 | 38 |
(1)求90分以上人数![]() 对小组序号
对小组序号![]() 的线性回归方程;
的线性回归方程;
附:回归方程为![]() ,其中
,其中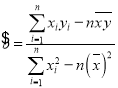 ,
,![]() .本题
.本题![]() ,
,![]() .
.
(2)能否在犯错误的概率不超过0.01的前提下认为7组与8组的成绩是否优秀(大于90分)与小组有关系.附部分临界值表:
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
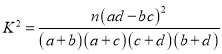 .
.
【题目】为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了![]() 人进行分析,得到如下列联表(单位:人).
人进行分析,得到如下列联表(单位:人).
经常使用 | 偶尔使用或不使用 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)根据以上数据,能否在犯错误的概率不超过![]() 的前提下认为
的前提下认为![]() 市使用共享单车的情况与年龄有关;
市使用共享单车的情况与年龄有关;
(2)(i)现从所选取的![]() 岁以上的网友中,采用分层抽样的方法选取
岁以上的网友中,采用分层抽样的方法选取![]() 人,再从这
人,再从这![]() 人中随机选出
人中随机选出![]() 人赠送优惠券,求选出的
人赠送优惠券,求选出的![]() 人中至少有
人中至少有![]() 人经常使用共享单车的概率;
人经常使用共享单车的概率;
(ii)将频率视为概率,从![]() 市所有参与调查的网友中随机选取
市所有参与调查的网友中随机选取![]() 人赠送礼品,记其中经常使用共享单车的人数为
人赠送礼品,记其中经常使用共享单车的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式: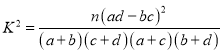 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
