题目内容
直线L:
+
=1与椭圆E:
+
=1相交于A,B两点,该椭圆上存在点P,使得△PAB的面积等于3,则这样的点P共有( )
| x |
| 4 |
| y |
| 3 |
| x2 |
| 16 |
| y2 |
| 9 |
| A、1个 | B、2个 | C、3个 | D、4个 |
分析:设出P1的坐标,表示出四边形P1AOB面积S利用两角和公式整理后.利用三角函数的性质求得面积的最大值,进而求得△P1AB的最大值,利用6√2-6<3判断出点P不可能在直线AB的上方,进而推断出在直线AB的下方有两个点P,
解答: 解:设P1(4cosα,3sinα)(0<α<
解:设P1(4cosα,3sinα)(0<α<
),即点P1在第一象限的椭圆上,考虑四边形P1AOB面积S,
S=S△OAP1+S△OBP1=
×4(3sinα)+
×3(4cosα)=6(sinα+cosα)=6
sin(α+
),∴Smax=6
.
∵S△OAB=
×4×3=6为定值,
∴S△P1AB的最大值为6
-6.
∵6
-6<3,
∴点P不可能在直线AB的上方,显然在直线AB的下方有两个点P,
故选B.
 解:设P1(4cosα,3sinα)(0<α<
解:设P1(4cosα,3sinα)(0<α<| π |
| 2 |
S=S△OAP1+S△OBP1=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
∵S△OAB=
| 1 |
| 2 |
∴S△P1AB的最大值为6
| 2 |
∵6
| 2 |
∴点P不可能在直线AB的上方,显然在直线AB的下方有两个点P,
故选B.
点评:本题主要考查了直线与圆锥曲线的关系.考查了学生分析问题和解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

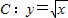 与直线l:y=x-c的交点为P(异于原点O).在曲线C上取一点P1(x1,y1),过点P1作P1Q1平行于x轴,交直线l于Q1,过点Q1作Q1P2平行于y轴,交曲线C于P2(x2,y2);接着过点P2作P2Q2平行于x轴,交直线l于Q2,过点Q2作Q2P3平行于y轴,交曲线C于P3(x3,y3);如此下去,可得到点P4(x4,y4),P5(x5,y5),…,Pn(xn,yn),设点P坐标为
与直线l:y=x-c的交点为P(异于原点O).在曲线C上取一点P1(x1,y1),过点P1作P1Q1平行于x轴,交直线l于Q1,过点Q1作Q1P2平行于y轴,交曲线C于P2(x2,y2);接着过点P2作P2Q2平行于x轴,交直线l于Q2,过点Q2作Q2P3平行于y轴,交曲线C于P3(x3,y3);如此下去,可得到点P4(x4,y4),P5(x5,y5),…,Pn(xn,yn),设点P坐标为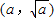 ,x1=b,0<b<a.
,x1=b,0<b<a.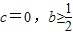 时,求证:
时,求证: .
. 与直线l:y=x-c的交点为P(异于原点O).在曲线C上取一点P1(x1,y1),过点P1作P1Q1平行于x轴,交直线l于Q1,过点Q1作Q1P2平行于y轴,交曲线C于P2(x2,y2);接着过点P2作P2Q2平行于x轴,交直线l于Q2,过点Q2作Q2P3平行于y轴,交曲线C于P3(x3,y3);如此下去,可得到点P4(x4,y4),P5(x5,y5),…,Pn(xn,yn),设点P坐标为
与直线l:y=x-c的交点为P(异于原点O).在曲线C上取一点P1(x1,y1),过点P1作P1Q1平行于x轴,交直线l于Q1,过点Q1作Q1P2平行于y轴,交曲线C于P2(x2,y2);接着过点P2作P2Q2平行于x轴,交直线l于Q2,过点Q2作Q2P3平行于y轴,交曲线C于P3(x3,y3);如此下去,可得到点P4(x4,y4),P5(x5,y5),…,Pn(xn,yn),设点P坐标为 ,x1=b,0<b<a.
,x1=b,0<b<a. 时,求证:
时,求证: .
.